Question
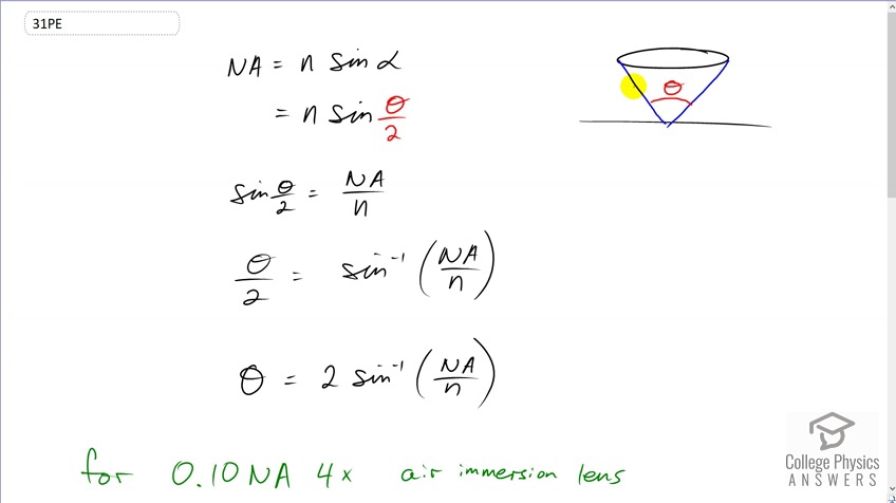
You are using a standard microscope with a 0.10NA 4x objective and switch to a 0.65NA 40x objective. What are the acceptance angles for each? Compare and comment on the values. Which would you use first to locate the target area on of your specimen?
Final Answer
0.10NA lens:
0.65NA lens:
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 31 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
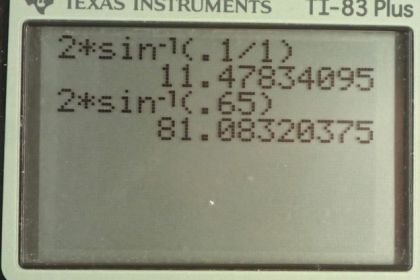
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The acceptance angle for the objective lens on a microscope is the angle at the tip of this cone of light that is entering the lens and the bigger this angle is, the bigger the cone of light enter in the lens and the better the resolution in terms of seeing detail. And now, the smaller the angle, the better at locating a specific position in the sample. So, we're going to find the acceptance angle for these two different lenses and we have a 0.10 numerical aperture lens and then a 0.65 numerical aperture lens. We're assuming that they're both in air, since it doesn't tell us otherwise, in which case our index of refraction is one. But first, let's find our formula for the acceptance angle. So, we're given that the numerical aperture is the index of refraction of the medium through which the light is traveling, which is air in this case times sine of alpha, which we're told is half of the acceptance angle. And so, we'll divide both sides by the index of refraction N and we get sine of half the acceptance angle is numerical aperture divided by index of refraction and then take the inverse sine of both sides to get Theta over two is inverse sine of that. Then, multiply both sides by two and you end up with the acceptance angle Theta is two times inverse sine of numerical aperture divided by index of refraction. So, in the first case, we have the acceptance angle is two times the inverse sine of 0.1 numerical aperture divided by the index of refraction of air which is one, giving us an acceptance angle of 11 degrees. And then in the second case, he acceptance angle is two times inverse sine of 0.65 numerical aperture divided by one, which is 81 degrees. So, we should first use the 0.1 numerical aperture lens to locate the object because it has a smaller acceptance angle, and so it sees only a small piece of the sample at a time and so for that reason, it's better to be able to identify the place where the target is. And then after finding it, you would switch to this lens to get a higher resolution view of it since the acceptance angle is larger, it's getting a larger cone of light. And with that, it can create a higher resolution image to see more detail.