Question
A severely myopic patient has a far point of 5.00 cm. By how many diopters should the power of his eye be reduced in laser vision correction to obtain normal distant vision for him?
Final Answer
-20 D
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 11 (Problems & Exercises)
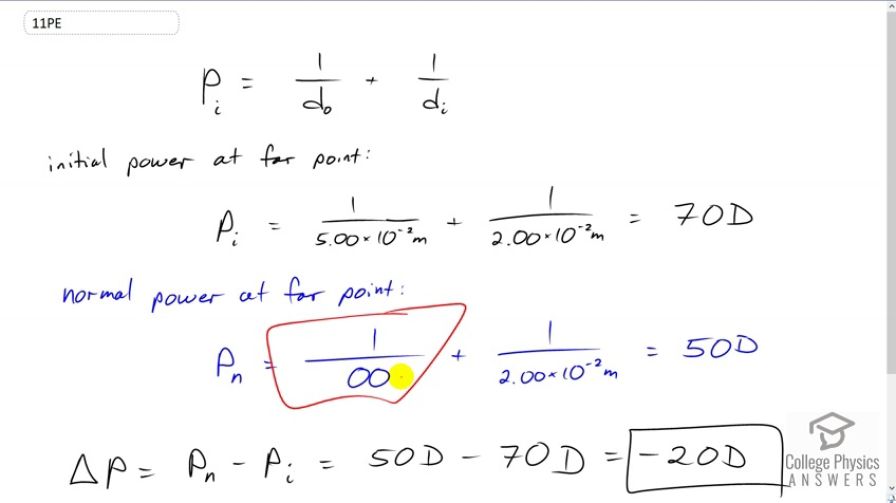
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This myopic patient has a far point that is not infinity. Normally, we can see things that are any distance away. Like, it can be really far away and we'll take it to be infinitely far away as the far point for normal vision. Things don't become blurry by being far away, normally. But for someone who has myopia, things that are far away are blurry. And so, they have a far point. For most people, the far point is not really a number, it's just a concept. It's this infinity. But for people with myopia, the far point is a specific distance beyond which things are blurry. And so, for this person initially, their eye has a certain power which is one over object distance plus one over image distance and this object distance is five centimeters for this person, which is surprisingly close. They're severely myopic. So, the image distance is two centimeters because that's the lens retina distance. And, we'll find the initial power by adding the reciprocals of the object distance and image distances together to get a power of 70 diopters, writing both distances in meters in order to have diopters as our units for power. Now, for normal vision, the far point should be infinity, and so this becomes zero. And then, we add to that one over the image distance of two times ten to the minus two meters to get a normal power of 50 diopters when the eye is relaxed and looking in the distance. So that means, they require some laser surgery that will change their power by 50 diopters minus 70 diopters, or negative 20 diopters. So, they need to reduce the power of their eye in order to have normal vision.
