Question
The contact lens prescription for a mildly farsighted person is 0.750 D, and the person has a near point of 29.0 cm. What is the power of the tear layer between the cornea and the lens if the correction is ideal, taking the tear layer into account?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 20 (Problems & Exercises)
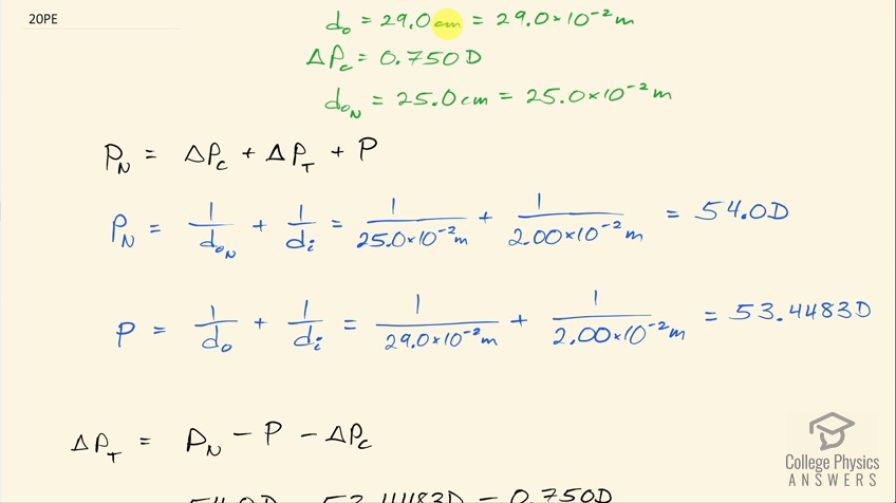
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A person's near point without any correction and no contact lenses is 29.0 centimeters so the closest thing they can possibly see is 29.0 centimeters away, they want to have a near point of 25.0 centimeters because that's what the normal near point is and so they have contact lenses providing a correction of 0.750 diopters and that's not the full correction required though because the tear layer has some correction as well and the question is what change in power is caused by the tear layer? So the normal power for looking at something as close as possible— 25.0 centimeters away— is the result of all these different powers; there's the original power of the eye with nothing involved— no tear layer or contact lenses— and we have added to that the correction caused by the contact lenses and then plus the correction caused by the tear layer and this ΔP T is what we need to solve for and we'll do that by figuring out what the other terms are in this equation. So the power for normal vision when looking at the near point, is 1 over the object distance at the near point plus 1 over the image distance. So that's 1 over 25.0 centimeters, written as 25.0 times 10 to the minus 2 meters plus 1 over the lens-retina distance, which is 2.00 centimeters normally which is 2.00 times 10 to the minus 2 meters and that's a power of 54.0 diopters so normal vision has this power. The power of the person's eye with no tear layer and no contact lenses involved is 1 over their near point of 29.0 centimeters written as 29.0 times 10 to the minus 2 meters plus this same 1 over the same image distance because that's inside the eye between the lens and the retina and this is 53.4483 diopters. So we can rearrange this equation to solve for ΔP T and we'll subtract their unaided power P from both sides as well as the power coming from the contact lenses (oops) and then we have this line here. So the power of the tear layer is the normal power at the near point minus their unaided power at the near point minus the change in power due to the contact lenses. So that's 54.0 diopters minus 53.4483 diopters minus this positive 0.750 diopters—correction from the contact lens— this works out to negative 0.198 diopters is the correction caused by the tear layer.
