Question
Suppose a certain person’s visual acuity is such that he can see objects clearly that form an image high on
his retina. What is the maximum distance at which he can read the 75.0 cm high letters on the side of an airplane?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 4 (Problems & Exercises)
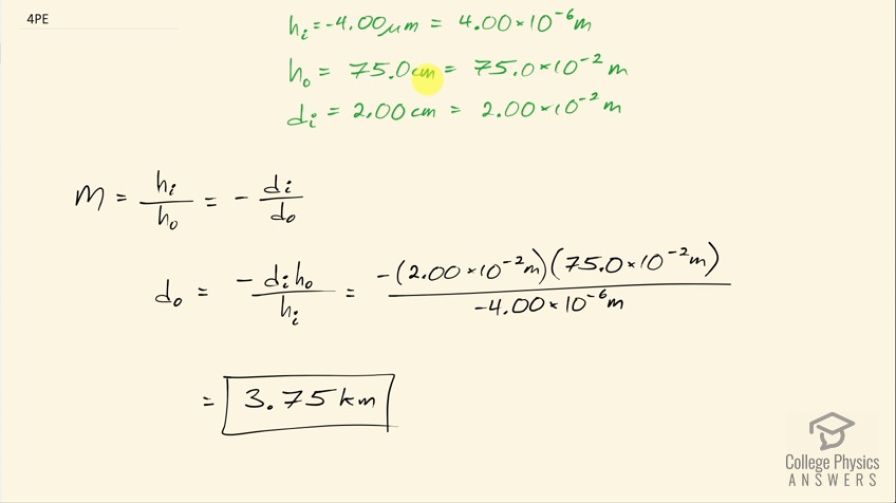
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We want to find the object distance for these letters on the side of an airplane and the letters are 75.0 centimeters high, which is 75.0 times 10 to the minus 2 meters and this object is going to make an image with a height of only 4.00 micrometers at its smallest on the retina and I put a negative here just to say that this is a real image and so it's going to be inverted compared to the object and that's just going to be helpful in our calculation here, which has a negative sign in our formula for magnification. The image distance we know because the lens-retina distance is the image distance and that's 2.00 centimeters and we know that magnification is the ratio of the image height to the object height and it's also the negative of the ratio of the image distance to the object distance. So we are gonna solve this for d o, which is the distance from the lens to the letters on the plane, we'll multiply both sides by d o and also multiply both sides by object height divided by image height and we end up with object distance is the negative of the image distance times the object height divided by the image height. So that's negative of 2.00 times 10 to the minus 2 meters— distance from the lens to the retina— times 75.0 times 10 to the minus 2 meters— height of the letters on the airplane— divided by negative 4.00 times 10 to the minus 6 meters, which is the size of the image on the retina... that is 3.75 kilometers is the maximum distance at which the person can read the letters.
