Question
A small telescope has a concave mirror with a 2.00 m radius of curvature for its objective. Its eyepiece is a 4.00 cm focal length lens. (a) What is the telescope’s angular magnification? (b) What angle is subtended by a 25,000 km diameter sunspot? (c) What is the angle of its telescopic image?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 36 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
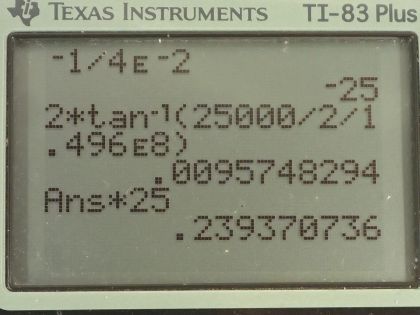
This is College Physics Answers with Shaun Dychko. A telescope has an objective mirror with a radius of curvature of 2.00 meters and I write that as negative because we are told that it's concave and it has an eyepiece focal length of positive 4.00 centimeters, which is 4.00 times 10 to the minus 2 meters and it's important to change the units here so that the units we are working with and these two different quantities are the same. So the angular magnification of the telescope is the negative of the objective focal length divided by the eyepiece focal length and we can take this radius of curvature for the objective mirror, divide it by 2 and that will give us the focal length of the objective mirror. So that's negative 2.00 meters divided by 2 which is negative 1.00 meters. So the angular magnification then is negative 1.00 meter divided by 4.00 times 10 to the minus 2 meters which is negative 25.0. Part (b) is asking what would the angular size be of a 25000 kilometer diameter sunspot? So we know that the distance between the Earth and the Sun is 1.496 times 10 to the 8 kilometers and if this is an isoceles triangle that I have drawn here, where this side equals this side so that means if we create an altitude for this triangle, which is to say a line that is perpendicular to the base that altitude is going to bisect this angle and so we have this angle α in this triangle where this leg that's opposite α is half the diameter of the sunspot and this distance here is the Earth-Sun distance. We can figure out this angle α by saying tangent of that angle is the opposite which is sunspot diameter divided by 2 all over the Earth-Sun distance or you can say d over 2 times d ES and then solve for α and it's the inverse tangent then of this fraction when you take the inverse tangent of both sides here and then the angle Θ subtended at the Earth by this sunspot is going to be 2 times this angle α and so that's 2 times the inverse tangent of 25000 kilometers divided by 2 times 1.496 times 10 to the 8 kilometers which is 9.57 times 10 to the minus 3 degrees. Part (c) is asking us what is the angle of its telescopic image? So the angular magnification can also be written as the angular size view to the telescope, which is labeled Θ prime divided by the angular size when viewed unaided and so we'll solve for Θ prime by multiplying both sides by Θ and so we get Θ prime then is the angular magnification times the unaided angular size. So that's negative 25.0 times 9.57 times 10 to the minus 3 degrees, which is 0.239 degrees.