Question
A mother sees that her child’s eyeglasses prescription is 0.750 D, for eyeglasses that are positioned 2.20 cm from her eyes. What is the child’s near point?
Final Answer
29.7 cm
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
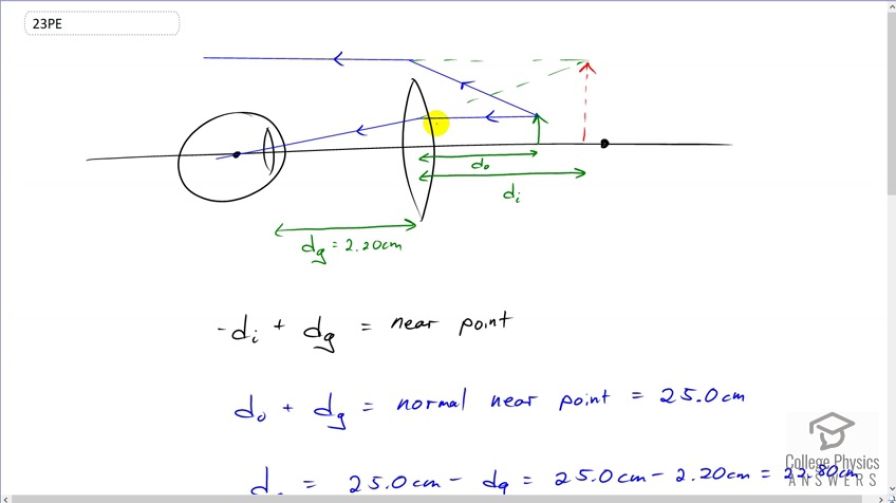
This is College Physics Answers with Shaun Dychko. This child's eyes are far-sighted which means they have difficulty seeing things that are close. So, that means they need some glasses that will reposition an object at a further position away so that they can see it properly. So, this lens creates an image of the object, which is here, and this is at the near point of the child's eyes. So, this is the distance we're trying to find in this question. So, this image is going to be at an image distance with respect to their glasses lens, and so we'll call that Di. And then, we have Dg for glasses, which is the distance between the glasses and the child's eyes, which is 2.2 centimeters. And so, this near point, this distance between the closest position that they can see and their eye is going to be this glasses distance plus the magnitude of the image distance. And, I know that this image is going to be a negative number since it's on the same side of the lens as the object, which makes it a virtual image, and so, it's going to be negative, so I put a negative sign in front of that to end up making it positive. So, the object distance plus the glasses distance is the normal near point. So, the glasses are designed so that when an object is here, the child will be able to see it. And so, this is an arbitrary number, really, but it's just what the optometrist considers to be a normal near point. And, that's 25 centimeters. And so, from that we can figure out what the object distance is. It's going to be 25 minus the separation between the glasses and the eyes. So, that's 25 minus 2.2, which is 22.8 centimeters. Now, we can use this power formula to figure out what the image distance is between the lens and the image that it creates. And, we'll subtract one over the object distance from both sides and then switch the sides around and then take both sides to the power of negative one to solve for the image distance. So, the image distance is the power minus one over object distance to the negative one. So, that's 0.75 diopters that the question tells us minus one over 22.8 times ten to the minus two meters object distance all to the negative one which is negative 27.5 centimeters. And so, the near point is going to be this distance between the glasses and the object. And, we'll take its magnitude and then plus the distance between the glasses and the eye. And, this works out to 29.7 centimeters is the near point of the child's eyes. So, without the glasses, they would require the object to be here in order to see it. And then with the glasses, they can bring the object closer to here and then they're able to see the image at that location of the near point.
