Question
(a) Where does an object need to be placed relative to a microscope for its 0.500 cm focal length objective to produce a magnification of –400 ? (b) Where should the 5.00 cm focal length eyepiece be placed to produce a further fourfold (4.00) magnification?
Final Answer
- from the objective lens.
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
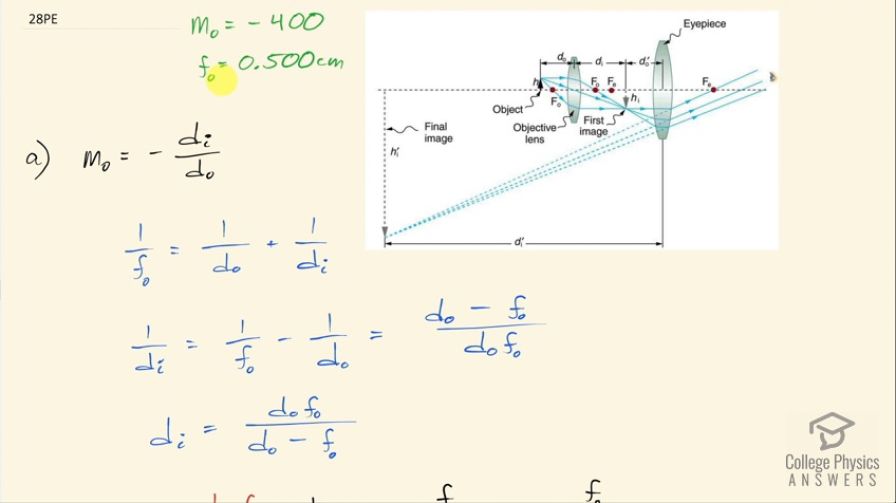
This is College Physics Answers with Shaun Dychko. A compound microscope has an objective with a magnification of negative 400 and the objective has a focal length of 0.500 centimeters and the question we are asked is knowing that where should the object be placed compared to the objective lens so we are finding this distance d o and I am going to use the same symbols as this figure has in all of my work here so d o is the object distance for the objective and d o with this prime symbol on it— this little apostrophe— is going to be the object distance from the eyepiece. Okay but in this part (a), we are dealing only with the objective lens. So the magnification of the objective is the negative of the image distance divided by the object distance and we also have this thin lens equation that says 1 over the objective focal length is 1 over the object distance plus 1 over the image distance and we are going to combine these two to figure out what is d o. So we'll solve for d i eventually... first, we have 1 over d i is 1 over the focal length minus 1 over the object distance because we want to replace d i in this magnification formula and then we'll have a formula containing only d o, the focal length and the magnification and we'll solve for d o. Okay! So if we want to have a common denominator here, we could multiply this term by d o divided by d o and this term by f o over f o and then we have d o minus f o all over d o times f o is 1 over d i and then raise both sides to the exponent negative 1 and we get d i is d of o over d o minus f o so this exponent negative 1 flips both of these fractions and then this becomes something we can replace in our magnification formula. So replacing d i with d of o over d o minus f o and then multiplying it by the denominator here because we don't want to have a fraction divided by a fraction since that's a bit messy looking so I am going to multiply by 1 over d o. And the d o's cancel, leaving us with f o over d o minus f o negative and then because that negative is a bit messy, let's apply it to the denominator so we have f o positive minus d o on the bottom. And then multiply both sides by f o minus d o and then we have and then also divide both sides by the magnification and we have f o minus d o equals f o divided by m o. And then add d o to both sides and subtract f o over m o from both sides and you have d o on one side equals f o minus f o over m o on the other side. I have done the algebra differently in part (b) by the way because part (b) asks us the same question for the eyepiece lens and so you have another way to look at it in a second. But anyway... the object distance from the objective is 0.500 centimeters—focal length of the objective—minus 0.500 centimeters focal length divided by negative 400 magnification and that is 0.501 centimeters. So this distance between the objective and the physical object is going to be 0.501 centimeters. Part (b) asks us where should the 5.00 centimeter focal length eyepiece be placed to produce a 4.00-fold further magnification? So first we need to figure out what is going to be the d o prime what is gonna be this object distance from the eyepiece because after we know that, we'll add it to the image distance from the objective and this total will be the distance between the eyepiece and the objective. So the eyepiece focal length is 5.00 centimeters, the eyepiece magnification is 4.00 times and from this, we are gonna figure out d o prime. So here's the thin lens equation for the eyepiece: 1 over the eyepiece focal length is 1 over image distance prime— this is the image distance for the eyepiece— plus 1 over the object distance for the eyepiece so that's d o prime there. Magnification for the eyepiece is negative d i prime over d o prime and we can solve this for d i prime by multiplying both sides by d o prime negative and we get d i prime is negative m ed o prime so this can be substituted into the thin lens equation and this is what makes the technique here in part (b) different algebraically speaking from the technique in part (a) is I am substituting from the magnification formula into the thin lens equation. So we have negative m ed o prime written in place of d i prime and our job here is to solve for d o prime by the way, we'll factor d o prime out from both of these terms and we get this line. So 1 over f e equals 1 over d o prime times 1 minus 1 over m e switch these terms around to put the negative term on the right side here and then multiply both sides by d o prime times f e and so the f e cancels on the left and the d o prime cancels on the right and we are left with d o prime equals f e times 1 minus 1 over m e which is the same sort of formula we had here, I just didn't factor out the focal length but the object distance is, you know, the same here... but different numbers down here of course. So this is the object distance for the eyepiece and it's going to be the 5.00 centimeter focal length of the eyepiece times 1 minus 1 over 4.00 times magnification of the eyepiece and that is 3.75 centimeters. So we found this distance here just now and the total distance from the objective lens to the eyepiece then is the image distance of the objective lens plus this object distance of the eyepiece. So we have to find d i now and the magnification of the objective is well, it's the negative of d i over d o but this is negative 400 magnification for the objective so I guess I should be plugging in negative 400 here. In any case... it is the magnitudes we are interested in here anyway. So we multiply both sides by negative d o and you have d i is negative m o times d o. So the negative from the formula times the negative 400 magnification of the objective times 0.50125 centimeters— object distance that we found in part (a)— gives us 200.5 centimeters is the image distance for the objective. So that 200.5 centimeters plus the 3.75 centimeters object distance for the eyepiece is a total of 204.25 centimeters. So the eyepiece will be placed 204 centimeters from the objective lens.

