Question
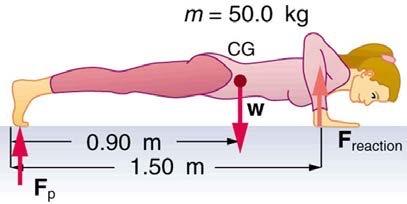
(a) What force should the woman in Figure 9.46 exert on the floor with each hand to do a push-up? Assume that she moves up at a constant speed. (b) The triceps muscle at the back of her upper arm has an effective lever arm of 1.75 cm, and she exerts force on the floor at a horizontal distance of 20.0 cm from the elbow joint. Calculate the magnitude of the force in each triceps muscle, and compare it to her weight. (c) How much work does she do if her center of mass rises 0.240 m? (d) What is her useful power output if she does 25 pushups in one minute?
Final Answer
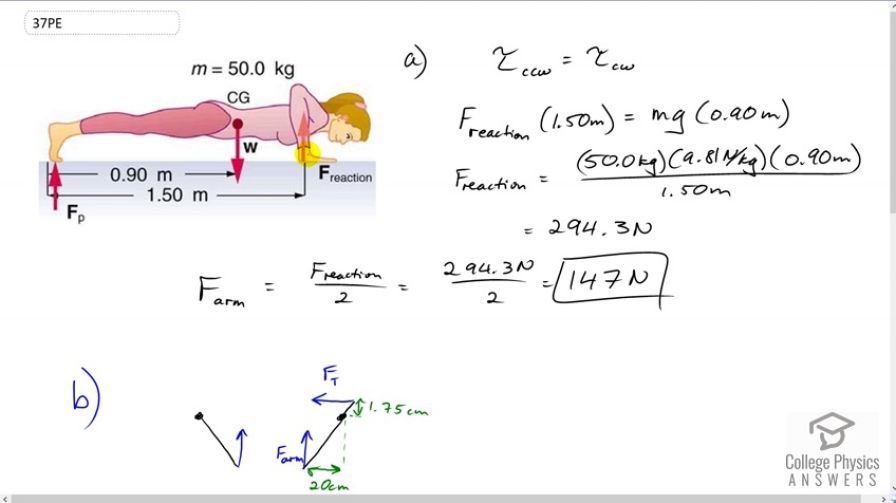
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 9, Problem 37 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to figure out with what force does she push down on the floor. In this picture we have this reaction force with an arrow pointing up and that's the newtons' Third Law counterpart to the force that her arm applies on the floor. This is the force that the floor applies on her arm upwards. That force upwards multiplied by its lever arm of 1.5 meters has to equal the weight downwards multiplied by its lever arm of 0.9 meters. We're saying that the counter-clockwise torques have to equal the clockwise torques in order to be moving at constant speed. So divide both sides by 1.5 here and then we get the reaction force is 50 kilograms times 9.81 newtons per kilogram times 0.9 meters divided by 1.5 meters. That gives 294.3 newtons but that's the total force upwards needed and she has two arms each of which will be exerting half of that I suppose and that works out to 147 newtons. In part B, we have her hands are a little bit closer together underneath her chest so her elbows are sort of sticking out here and her hands are positioned 20 centimeters in towards each other compared to where her elbow is. So there is a torque exerted about her elbow by the force on the arm by the floor and that torque is going to be force of the arm times 20 centimeters, we're told this is lever arm, and that torque has to equal the torque due to the triceps with its lever arm of 1.75 centimeters. So we divide both sides by 1.75 here and we get the force in a single tricep is 147 newtons which is the force exerted on a single hand or arm, times 20 centimeters divided by 1.5 centimeters giving us 1680 newtons. The work done is the force of gravity multiplied by the displacement of her center of mass. We don't take the force exerted on the arm because we don't really know what this distance of the front of her body where the arm is acting, we don't know what distance over which that force occurs. But we do know the distance over which the force of gravity is acting there and we're told that its center of mass moves 0.24 meters. So we multiply the weight 50 kilograms times 9.8 by that 0.24 meters to get 118 joules. The power output is going to be that work multiplied by 25 times with 25 push-ups, and divide that by a minute which we have to convert into seconds in order to have units of watts. So we multiply one minute by 60 seconds per minute and we get 49 watts of power.

