Question
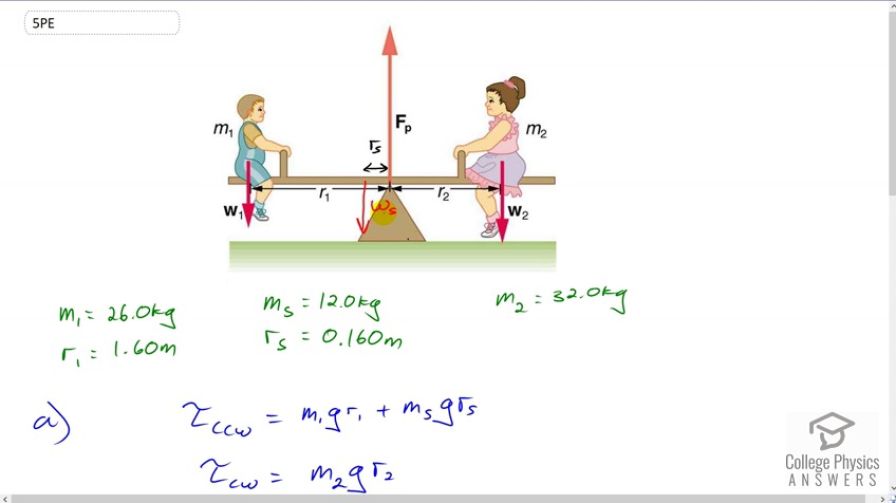
Repeat the seesaw problem in Example 9.1 with the center of mass of the seesaw 0.160 m to the left of the pivot (on the side of the lighter child) and assuming a mass of 12.0 kg for the seesaw. The other data given in the example remain unchanged. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium.
Example 9.1
The two children shown in Figure 9.10 are balanced on a seesaw of negligible mass. (This assumption is made to keep the example simple—more involved examples will follow.) The first child has a mass of 26.0 kg and sits 1.60 m from the pivot.(a) If the second child has a mass of 32.0 kg, how far is she from the pivot? (b) What is , the supporting force exerted by the pivot?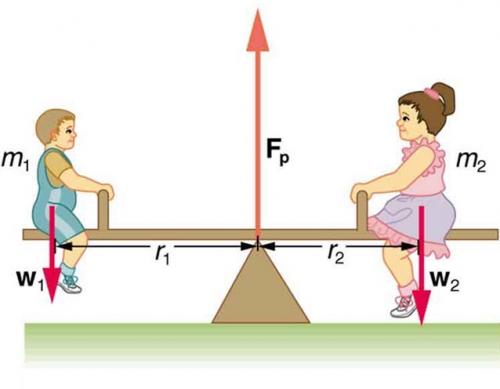
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 9, Problem 5 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This is the same picture as we have in example 9.1, with the addition of a new weight here due to the seesaw. So it’s w subscript s for seesaw, and it’s positioned at some distance from the pivot r subscript s, so this is the center of mass of the seesaw. And it’s going to exert a counter-clockwise torque in the same direction as the torque exerted by this boy. We know that for static equilibrium to occur, we have the total counter-clockwise torque has to equal the clockwise torque. And so we create expressions here for each. So we have the weight of the boy multiplied by his distance from the pivot and then add to that the torque due to the seesaw, and that’s going to equal the clockwise torque due to the girl which is m2 times g times her distance from the pivot r2. And we equate these two, and then we solve for r2 and we also divide both sides by g and it will cancel everywhere. So we have the distance that the girl needs to sit from the pivot is going to be m1 r1 plus ms rs, all divided by m2. So it’s 26 kilograms mass of the boy times 1.6 meters, plus 12 kilograms mass of the seesaw times 0.16 meters, divided by 32 kilograms mass of the girl, and that gives a position of 1.36 meters from the pivot. The next question is what should this force due to the pivot be, and by the way, this force did not appear in our torque calculation because the level arm for this force is zero because it’s positioned at the pivot. And so it doesn’t exert any torque above the pivot, but it does exert a force obviously, that’s what supporting this whole seesaw and the kids. And so the total force upwards, which is consisting only of this one force due to the pivot, has to equal the total force down, which is the weight of the boy and the girl and the seesaw. We can factor out the g there, common factor. So we have the force of the pivot is g times the total mass, so that’s 9.8 newtons per kilogram gravitational field strength, multiplied by 26 kilograms mass of the oy plus 32 kilograms mass of the girl plus 12 kilograms mass of the seesaw, giving 686 newtons.
Comments
So does moving the pivot point to the left not effect the torque? I thought r1 would be 1.60m - 0.160m since it moved to the left.
Hi emgem, the wording in this question is a bit sneaky. It isn't the pivot that moves to the left, but rather the center of mass of the seasaw that moves to the left. In other words, the distribution of mass of the seasaw changes such that it isn't uniform anymore - there must be a bulge of material on the left side.
Hope this helps,
Shaun


