Question
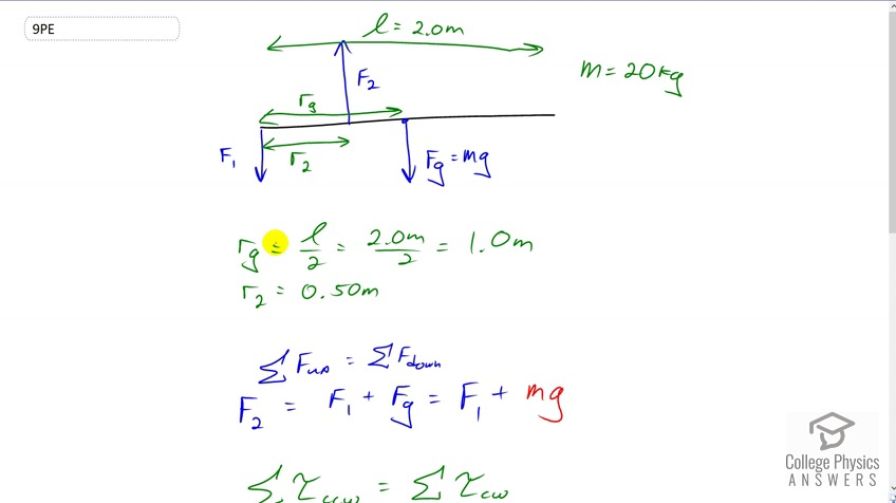
A person carries a plank of wood 2.00 m long with one hand pushing down on it at one end with a force and the other hand holding it up at 50.0 cm from the end of the plank with force . If the plank has a mass of 20.0 kg and its center of gravity is at the middle of the plank, what are the magnitudes of the forces and ?
Final Answer
,
Solution video
OpenStax College Physics, Chapter 9, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a two meter long plank of wood and we’re told that the center of mass is exactly in the center, so that’ll be at a position two meters divided by two, which is 1.0 meters from an end. That’s also going to be the level arm of this gravity force when we calculate its torque above the pivot here at the end. We don’t have to choose the pivot to be there but it is convenient to do so because when we have our torque equation, it’s going to consist only of force F2 and Fg and it will not have force F1 in it because the level arm for force one is zero if we choose this to be the pivot point. So, what else do we know. We know that r2 is 0.5 meters, that’s the level arm for force two, and the mass of the plank is 20 kilograms. So the first condition for static equilibrium is that the total net forces have to be zero. So the total forces up have to equal the total forces down. And there's only one force upwards, that’s F2, and there are two forces downwards, F1 plus Fg, and Fg is mg. That’s as far as we can go there because there are two unknowns and so we can’t do anything more with that equation, F2 and F1 are both things we don’t know. Now let’s consider torque. The total counter-clockwise torque has to equal the total clockwise torque. And F2 is exerting a torque that is counter-clockwise, so we have F2 multiplied by r2 on the left side, on the right side we have mg times rg is the torque exerted by gravity, and this has only one unknown there which is F2 so we’ll solve for it by dividing both sides by r2. And so we have force two is mg, level arm of gravity divided by level arm of force two, so that’s 20 kilograms times 9.8 newtons per kilogram times one meter divided by 0.5 meters which gives 392 newtons. Then we can rearrange this formula where we talked about net force and solve it for F1 by subtracting mg from both sides and we get that F1 is F2 minus mg, so that’s 392 newtons that we just calculated minus 20 kilograms times 9.8, giving us 196 newtons.
