Question
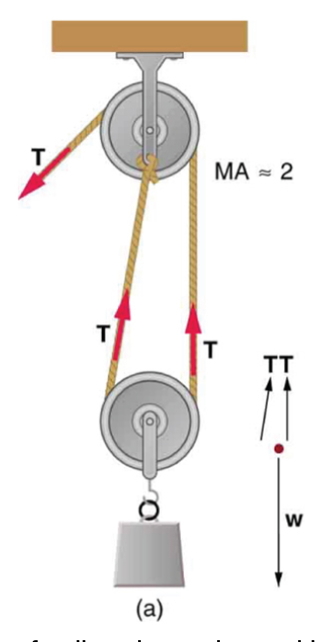
If you used an ideal pulley of the type shown in Figure 9.25(a) to support a car engine of mass 115 kg , (a) What would be the tension in the rope? (b) What force must the ceiling supply, assuming you pull straight down on the rope? Neglect the pulley system’s mass.
Final Answer
Solution video
OpenStax College Physics, Chapter 9, Problem 24 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This pulley system is a hoist for a car engine that has a mass of 115 kilograms and we can see that the mechanical advantage is 2 because the tension force that's being applied here is being exerted twice upwards on this engine and so there's one tension applied and that's being multiplied by 2 in the end and so that's where the mechanical advantage comes from. Okay! So mechanical advantage is defined as the output force divided by the input force and the input force is the tension in the rope and the output force is the total force on this bottom pulley so this is the output force and that's gonna be equal to the weight of the engine. So we substitute mg in place of F o and T in place of F i and then our job is to solve for T; we want to know the tension in the rope. So we multiply both sides by T over mechanical advantage so T is mg over MA. So that's 115 kilograms times 9.80 newtons per kilogram divided by 2 which is 564 newtons. In part (b), we are asked, what is the force applied by the ceiling upwards on this whole assembly? We can see that there's one force upwards in total on this assembly and there are two forces downwards: there's gravity downwards on the engine and then there's this applied force... this tension downwards as well and so those two are added together down and they have to together equal the force upwards on the ceiling. So that's 563.5 newtons—tension— plus 115 kilograms times 9.8 newtons per kilogram which is 1690 newtons in total exerted by the ceiling upwards on the whole assembly.
