Question
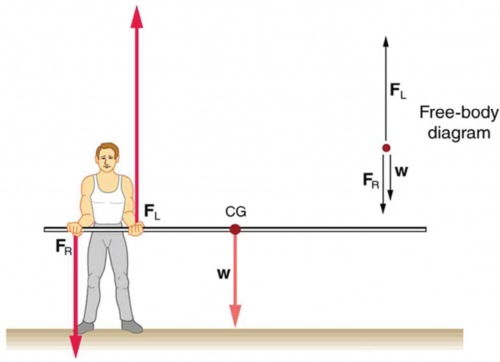
In Figure 9.20, the cg of the pole held by the pole vaulter is 2.00 m from the left hand, and the hands are 0.700 m apart. Calculate the force exerted by (a) his right hand and (b) his left hand. (c) If each hand supports half the weight of the pole in Figure 9.18, show that the second condition for equilibrium () is satisfied for a pivot other than the
one located at the center of gravity of the pole. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium described above.
Final Answer
- See video solution.
Solution video
OpenStax College Physics, Chapter 9, Problem 18 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
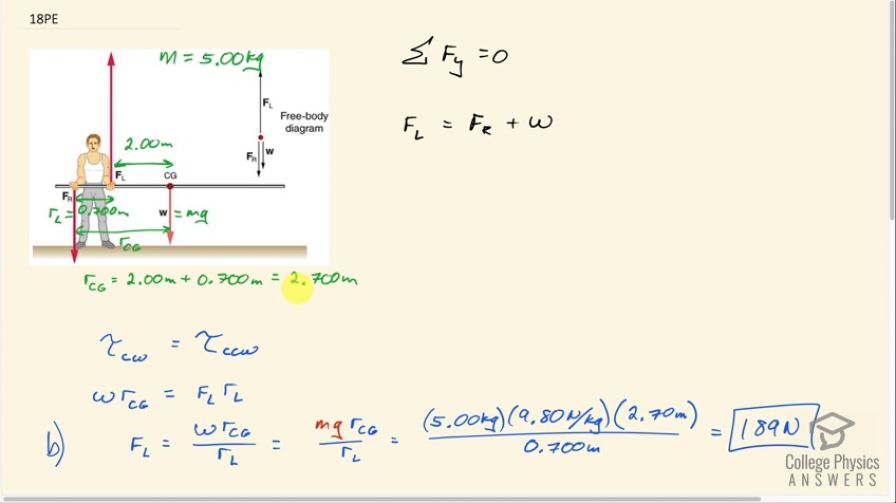
This is College Physics Answers with Shaun Dychko. This pole-vaulter is holding a 5.0 kilogram pole with a right hand a total of 2.70 meters from the center of gravity and the left hand is 2.0 meters from the center of gravity and we are going to use this first condition for equilibrium which is that that the vertical forces have to add up to zero which is to say that the up forces have to equal the total down forces so the left hand is exerting a force upwards and that has to equal the total of the right hand exerting a force down and gravity down. And then we'll talk about the torque as well which is the second condition of equilibrium: we'll say that the clockwise torque has to equal the counter-clockwise torque. So we are choosing a pivot to be at the right hand and you can choose pivot's either here, here or here— those are the logical spots— you can choose it to be anywhere actually but if you choose it to be on the position of one of the forces then you make that torque become zero in your calculations because it will have no lever arm. So we are choosing the pivot to be at the right hand so that the right hand force has no torque. So we have a clockwise torque due to gravity so that's w times the lever arm for gravity and that equals the counter-clockwise torque which is due to the left hand force multiplied by its distance from the right hand which is r L, lever arm for the left hand. Then we can solve for F L by dividing both sides by R L. So F L is the weight times the center of gravity's lever arm divided by the left hand's lever arm that's mgr CG over r L. So that's 5.0 kilograms times 9.8 newtons per kilogram times 2.7 meters divided by 0.700 meters which is 189 newtons. Then we can return to this equation here and solve for F R and we can do that by subtracting the weight from both sides. So F R is F L minus the weight— that's F L minus mg— so that's 189 newtons that we calculated before minus 5.00 kilograms times 9.80 newtons per kilogram which is 140 newtons. Then part (c) says, look at figure [9.18] where these hands are equally distant from the center of gravity on either side of it and calculate the torques and show that they add up to zero. So we'll take the pivot to be at the right hand say and we are also told that the left hand and the right hand are both exerting a force of half the weight upwards which makes sense if they are equidistant from the center of gravity. And then we'll talk about torque here: we are adding the counter-clockwise torque which is positive F L times R L minus the clockwise torque due to the weight so that's the weight multiplied by its center of gravity or the weight multiplied by the lever arm for the center of gravity I should say. And r L is 2 times r CG because this left hand is equally distant from the center of gravity compared to the right hand so we substitute 2 times r CG here. And then the left hand is exerting a force of the weight over 2 so we make that substitution and these 2's cancel leaving us with wr CG minus wr CG which is 0 as we expected.
