Question
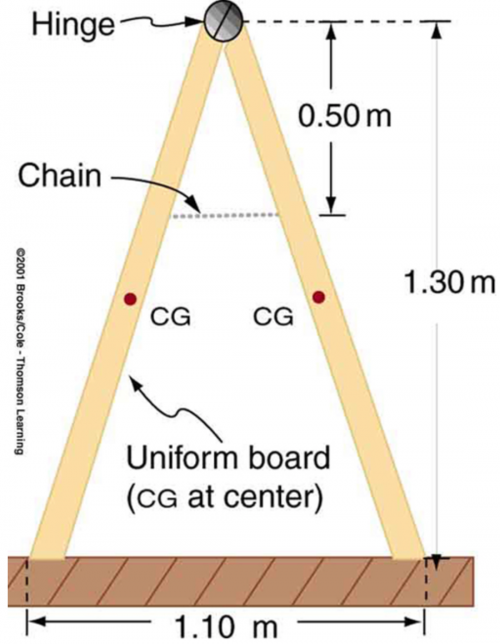
A sandwich board advertising sign is constructed as shown in Figure 9.34. The sign’s mass is 8.00 kg. (a) Calculate the tension in the chain assuming no friction between the legs and the sidewalk. (b) What force is exerted by each side on the hinge?
Final Answer
- horizontally
Solution video
OpenStax College Physics, Chapter 9, Problem 14 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This sandwich board is held together by this chain and it has a total mass of 8.00 kilograms and our job is to figure out what is the tension force on this chain. So we are going to figure out the normal force on the feet of this sandwich board and that can be found by saying that 2 times the normal force on each foot equals the total weight downwards and when we look at it that way, we don't have to worry about this hinge. Now the force exerted on a side by the hinge, there might be some angle to this hinge force— we don't really know— but we can ignore any vertical component to the hinge force because that's internal to both sides and it's not something we need to be concerned with when we talk about the normal force and gravity. Okay! So the normal force is half the weight, in other words. Now we can also talk about the horizontal forces— this is the first condition of equilibrium that we are talking about— and the horizontal forces have to balance out to total zero and so the x-component of this hinge force which is the hinge force times cosine of Θ has to equal the tension force to the left. And thirdly, we need a third equation since we have a hinge force that we don't know; a tension force that we don't know; and an angle that we don't know so we need a third equation to deal with three unknowns. So we have the second condition of equilibrium which is that the total clockwise torques have to equal the total counter-clockwise torques. So the counter-clockwise torques are due to the tension force in the chain and it has a distance r subscript T, this is the lever arm for the tension force of 1.30 meters total height minus this 0.50 meters from the hinge is where the chain's attached so that's 0.80 meters is the lever arm for the chain taking the pivot to be the foot of one side. And then we also have the weight exerting a counter-clockwise torque and it has a lever arm r W for weight of one-quarter this total width because we are told that this sandwich board is has a mass distribution that is uniform and so this hinge must be at the half-way point between the two feet and then this center of gravity has to be half-way point between the middle and the foot which makes it one-quarter of the way between the feet. So we have 1.10 meters—total distance between the feet—divided by 4 that's 0.275 meters is this r W. So we multiply that by the weight to get the additional counter-clockwise torque and then substituting mg over 2 for this F W because this is half the total weight and that has to equal the torque that's clockwise due to the hinge and so we have the lever arm of the hinge is r H, which is the height of the sandwich board, and multiplied by the hinge force times cos Θ because we want to get the component of the hinge force that's perpendicular to this lever arm. And then we substitute in F T in place of the F H cos Θ because our 'total force horizontally equaling zero' condition for equilibrium led us to that and so we can replace F H cos Θ with F T. And then we are gonna subtract F Tr T from both sides and then factor out the F T and we have F T times r H minus r T— of course, I have also switched the sides around too— and so all this equals mgr W over 2 and then divide both sides by r H minus r T. And so we have then that the tension force in the chain is mg lever arm of the weight divided by 2 times lever arm of the hinge minus the lever arm of the chain. So that's 8.00 kilograms times 9.80 newtons per kilogram times 0.275 meters divided by 2 times 1.30 meters minus 0.80 meters which is 21.6 newtons. And then in part (b), we want to find the hinge force and we can say that F H sin Θ plus the normal force equals the weight but we are... you know, this Θ is going to be zero because the weight is half the total weight of the sandwich board, mg over 2, the normal force is mg over 2 as well and that's what we figured out here and so that leaves nothing left over for this F H sin Θ it has to equal zero and of course, F H is not zero which means sin Θ is zero and that's true only when you have the angle being 0 degrees. Okay! So then we can say that the hinge force times cos Θ which is the horizontal component of the hinge force to the right has to equal the tension force to the left and then divide both sides by cos Θ but we have already established that this Θ is 0 and the cos of which is 1 and so the hinge force then is going to have the same magnitude as the tension force in the chain which is 21.6 newtons and that's horizontally and that will be to the right on the right hand side of the sandwich board and it will be to the left on the left hand side of the sandwich board.
Comments
How did you know that the counter clockwise torques are due to the chain and not the hinge? Why is the tension of the chain going counterclockwise while the hinge goes clockwise? Would the answer have been the same if the hinge went counterclockwise and the tension was clockwise?
Thank you!

