Question
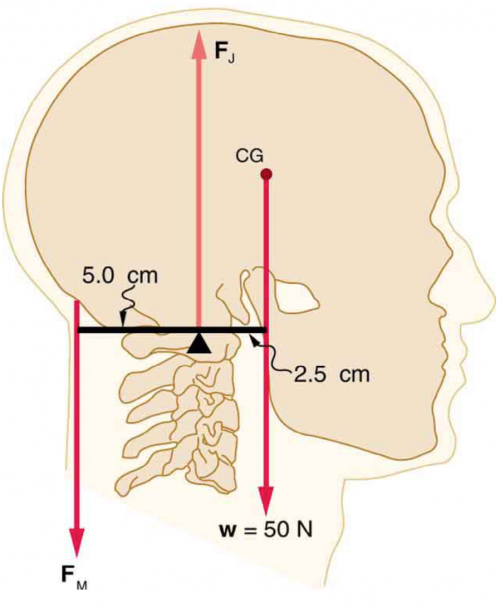
Even when the head is held erect, as in Figure 9.40, its center of mass is not directly over the principal point of support (the atlanto-occipital joint). The muscles at the back of the neck should therefore exert a force to keep the head erect. That is why your head falls forward when you fall asleep in the class. (a) Calculate the force exerted by these muscles using the information in the figure. (b) What is the force exerted by the pivot on the head?
Final Answer
Solution video
OpenStax College Physics, Chapter 9, Problem 32 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The atlanto-occipital joint is exerting a force upwards on the skull and there's a center of gravity positioned here which is exerting a torque about a pivot at this joint and it's 2.5 centimeters away and then there's neck muscles pulling straight down on this side exerting a counter-clockwise torque 5.0 centimeters from the pivot and when you say the two torque's have to be equal in order for the head to be stationary, and so we can solve for F M by dividing both sides by 5.0 centimeters. So by the way, this is the torque due to the weight of the head its weight multiplied by its lever arm— 2.5 centimeters— and here's the twerk due to the neck muscles the neck muscle force times 5 centimeters. So the neck muscle force then is the weight times 2.5 centimeters divided by 5.0 centimeters and it's okay to leave the units in centimeters instead of converting them into meters because since we are dividing these lengths, the centimeter units will cancel since they are the same. So we have 50 newtons times 2.5 divided by 5.0 which is 25 newtons is the force due to the muscles and that's downwards. The force due to this joint is the only force upwards and it has to balance the two forces downwards: force due to the muscle and the weight of the head. So it's going to be 25 newtons plus 50 newtons which is 75 newtons and that will be upwards.
