Question
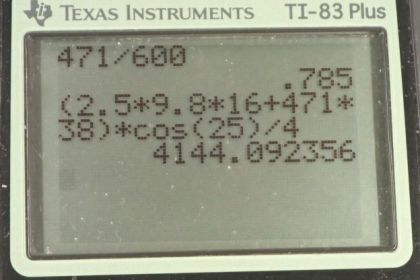
Suppose we replace the 4.0-kg book in Exercise 9.31 of the biceps muscle with an elastic exercise rope that obeys Hooke’s Law. Assume its force constant . (a) How much is the rope stretched (past equilibrium) to provide the same force as in this example? Assume the rope is
held in the hand at the same location as the book. (b) What force is on the biceps muscle if the exercise rope is pulled straight up so that the forearm makes an angle of with the horizontal? Assume the biceps muscle is still perpendicular to the forearm.
Final Answer
Solution video
OpenStax College Physics, Chapter 9, Problem 36 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
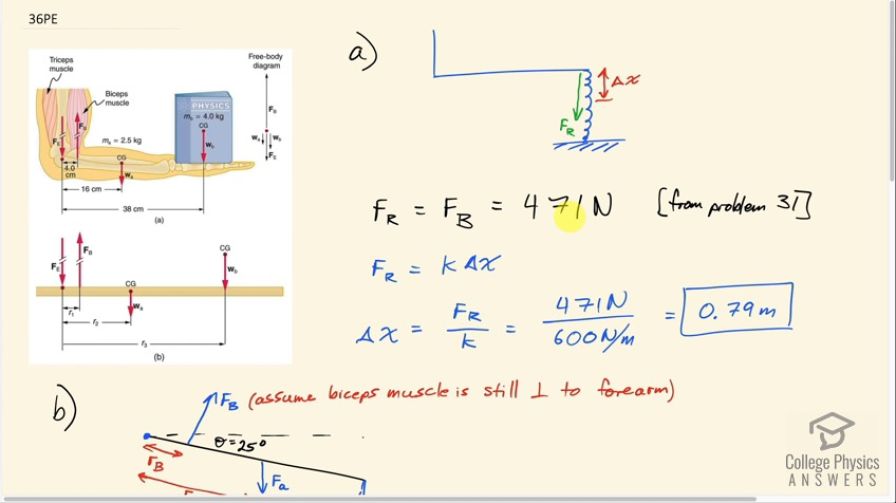
This is College Physics Answers with Shaun Dychko. We have seen this picture before in Problem 31 and in that problem, we had a solution of 471 newtons is the force that the bicep muscle has to pull upwards in order to hold on to this book. In that problem, the arm was actually at an angle of 120 degrees with respect to the bicep but it turns out that that didn't change the answer compared to the example in the textbook. Any case, what we are doing here is we are replacing the book with an elastic rope and this is meant to be stretched some amount that we have to find such that the force that the rope is pulling downwards is the same as the force the bicep is pulling upwards from this problem 31 so that's 471 newtons. So we use Hooke's law which is to say that the stretched rope is gonna have a force equal to the spring constant times the amount of stretching, Δx. And so we'll divide both sides by k and then switch the sides around and we solve for Δx is the force divided by the spring constant. So that's 471 newtons divided by 600 newtons per meter which is 0.79 meters. And then in part (b), we are told suppose that this hand is dropped so that the forearm makes an angle of 25 degrees with respect to horizontal and also assume that the bicep continues to be perpendicular to the forearm and what bicep force will there be now given this same rope force that we had in part (a)—471 newtons? So we are given these different lever arms from this picture and the bicep articulates 4.0 centimeters from the elbow and the center of gravity of the forearm is 16.0 centimeters from the elbow and the rope is going to be 38.0 centimeters from the elbow so those are the different lever arms here. Now we are gonna say that the counter-clockwise torque which is due to the bicep is going to equal the total clockwise torque which is due to the weight of the forearm and the rope and the counter-clockwise torque— since the bicep and lever arm are perpendicular— is just going to be the force multiplied by that length. But for the clockwise torques, we are going to need to consider the angle and there's a couple ways to think about it... I am gonna say let's imagine that we want to find the component of this lever arm that is perpendicular to the force. So imagine that this red line is the hypotenuse of a triangle like this and like this—it's a right triangle— here's the angle Θ with respect to horizontal and it's this length here that we are concerned with. This length is the component of the lever arm perpendicular to the force which is straight down and so we can find that component by multiplying this hypotenuse by cosine of the angle because this is the adjacent side. So we have that hypotenuse times cos Θ multiplied by the force and then same story for the rope torque— it's gonna be the rope force multiplied by its distance from the elbow multiplied by cos Θ— and then we'll solve for the bicep force by dividing both sides by the distance between the bicep's point of attachment and the elbow and so we have substituted the weight of the arm here for F a—that's mass times gravitational field strength. And then we have 2.50 kilograms— mass of the arm— times 9.80 newtons per kilogram times 16 centimeters and we can leave all our lengths in centimeters just because they are going to cancel anyway and so it's okay... you don't have to convert them to meters although we do normally convert things to mks units in our formula we won't do that this time just because we can see that they are going to cancel. Okay! So we add to that the force of the rope 471 newtons times 38 centimeters all that gets multiplied by cos 25 divided by 4.0 centimeters and that is 4.1 times 10 to the 3 newtons is going to be the bicep force.