Question
Suppose a man stands in front of a mirror as shown in Figure 25.50. His eyes are 1.65 m above the floor, and the top of his head is 0.13 m higher. Find the height above the floor of the top and bottom of the smallest mirror in which he can see both the top of his head and his feet. How is this distance related to the man’s height?
<b>Figure 25.50</b> A full-length mirror is one in which you can see all of yourself. It need not be as big as you, and its size is independent of your distance from it.
Figure 25.50 A full-length mirror is one in which you can see all of yourself. It need not be as big as you, and its size is independent of your distance from it.
Question by OpenStax is licensed under CC BY 4.0
Final Answer
hb=0.825 mh_\textrm{b} = 0.825 \textrm{ m} ht=1.72 mh_\textrm{t} = 1.72 \textrm{ m}

Solution video

OpenStax College Physics, Chapter 25, Problem 1 (Problems & Exercises)

vote with a rating of votes with an average rating of .
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 25, Problem 1 (PE) calculator screenshot 1

Comments

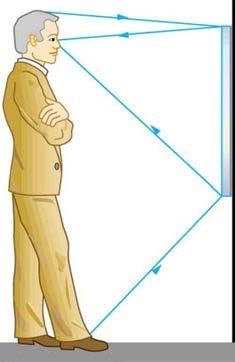
the length of the mirror is related to the height of a person by just being half of their height. Will this be true in all cases though?

This doesn't answer the last part of the question, "How is this distance related to the man’s height?"

Using ray-tracing and the law of reflection, the angle of incidence is equal to the angle of reflection, so the top of the mirror has to extend to at least halfway between their eyes and the top of their head. The bottom must go down to halfway between their eyes and the floor. This result is independent of how far they are standing from the wall.

Thank you for the comments be1988 and ryanzurrin. I have updated the final answer, which echos Ryan's correct response.
All the best with your studies,
Shaun

This video was updated on Jan. 16th, 2024.