Question
Referring to the electric room heater considered in the first example in this section, calculate the intensity of IR radiation in projected by the concave mirror on a person 3.00 m away. Assume that the heating element radiates 1500 W and has an area of , and that half of the radiated power is reflected and focused by the mirror.
Final Answer
Solution video
OpenStax College Physics, Chapter 25, Problem 63 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
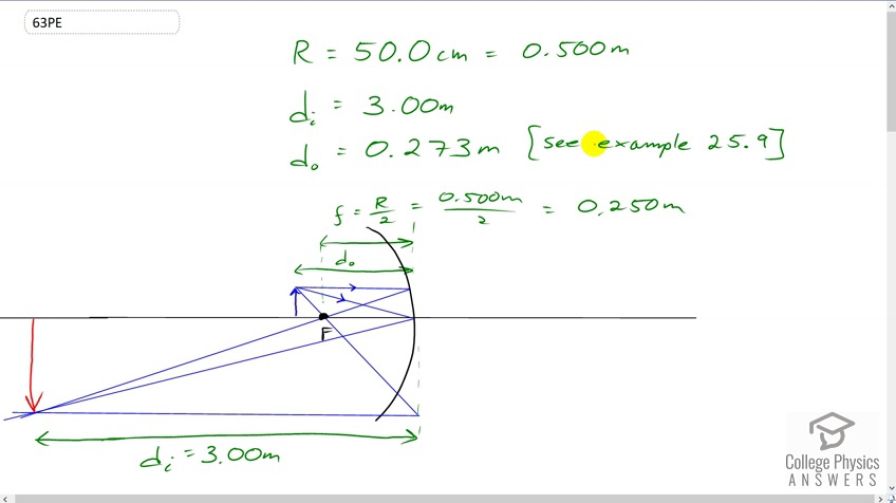
This is College Physics Answers with Shaun Dychko. There is a heater located here, some distance from a concave mirror, and we'll take this to be the object distance, which from example 25.9 we're told is 0.273 meters. And, there's going to be an image created at this position over here three meters away, this is where the person is going to be standing. And, we're going to figure out what is the intensity of radiation in the infrared band from this heater that they experience here. So, intensity is going to be the power distributed to this position divided by its area. So, we can figure out the focal length of this mirror by taking half of its radius of curvature. So, that's half of 0.5 meters which is 0.25 meters, and we're going to find the area of the image and then we'll take the power provided to the image divided by that area. And, we're told that the power is one-half the power output of the heater. This is just given to us in the question. The power delivered to the person is one-half the power produced. And so, we substitute both of these things into our intensity formula at the image. And then, so on and so on, we get the answer there. But, let's tell the story. So, the object area, so I have subscript O for object there, is going to be the object height times the object width. That's square heater. And then, the image area is going to be the image height times the image width. Now, magnification is the ratio of image height to object height. And, we can solve for the image height by multiplying both sides by Ho. And, we get then that image height is magnification times object height. And likewise, the image width will be magnification times the object width. And so, the area of the image is going to be the image height, magnification times object height, multiplied by image width, magnification times object width. So, I just made substitutions in here and here from this and this here. And, we see that the image area then is going to be magnification squared times object height times object width. And, this product is the object area. So, the image area is going to be magnification squared multiplied by the object area. Okay. And then, we have this formula for the intensity. It's the power delivered to the image divided by the image area. And then, we substitute M squared times object area in place of the image area here. And then, we're given that the power delivered to the image is half of the power output at the object. So, we substitute that in as well for Pi. And then, we need to figure out what the magnification is here. And so, magnification is negative of image distance divided by object distance and both of these things are known. And so, when we divide by this fraction, I'm going to instead multiply by its reciprocal and it's also squared. And so, we have one-half times power output of the object divided by object area, and then we're going to multiply by the reciprocal of the magnification squared. So, that's negative Do over DI squared. And, this works out to power produced by the heater times the object distance squared divided by two times the object area times the image distance squared. So, that's 1500 watts times 0.273 meters object distance squared divided by two times 100 square centimeters for the object area, which we have to convert into meters so we multiply one meter for every 100 centimeters two times. And then, multiply by the image distance of three meters squared, and this makes 621 watts per square meter is the intensity at the image, at the person.
