Question
(a) A narrow beam of light containing yellow (580 nm) and green (550 nm) wavelengths goes from polystyrene to air, striking the surface at a incident angle. What is the angle between the colors when they emerge? (b) How far would they have to travel to be separated by 1.00 mm?
Final Answer
Solution video
OpenStax College Physics, Chapter 25, Problem 31 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
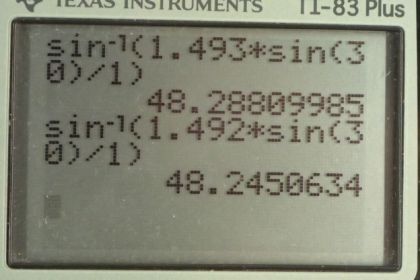
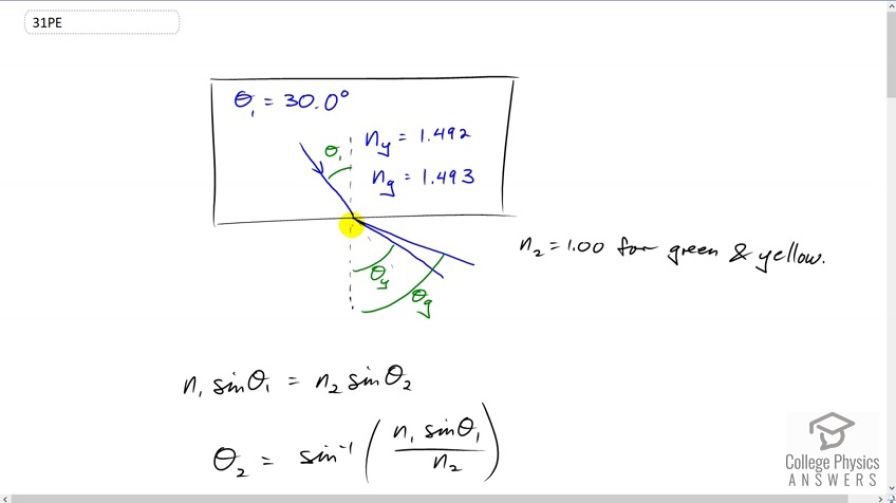
This is College Physics Answers with Shaun Dychko. A beam of light consisting of yellow and green travels through polystyrene and then emerges into air and has an angle of incidence of 30 degrees and when it has… when it goes into air, the angle of refraction will be different for the different colors and this is because the index of refraction for yellow and for green are different in polystyrene. The index of refraction for these two colors in the air is same. It’s always 1.00 in air but the fact that they are different within the polystyrene causes the angle of refraction to be different for two different colors and so the question is asking us for this little bit of angle in here that is different for the two rays. So, we call it delta theta and then part B of this question will ask us for how far would the beams have to travel through the air in order for them to be separated horizontally by distance of one millimeter. Okay. We’ll use Snell’s law to figure out what these angles of refractions are for yellow and for green and Snell’s law says that the incidence medium, the first medium, that it's traveling through index of refraction gets multiplied by sine of the angle of incidence, theta one, and that’s gonna equal the index of refraction in the second medium, we call it n two times sine theta two, the index… or the angle of refraction and then we can solve for theta two by dividing both sides by n two and then taking inverse sine on both sides and so theta two, the angle of refraction is the inverse sign of the first index of refraction times sine of the incident angle divided by the second index of refraction. Now, the delta theta, this difference in the angle of refraction for the two colors is gonna be the difference between the angle of refraction for green minus the angle of refraction for yellow and so we will calculate each of these now. So, theta g is gonna be inverse sine of 1.493 times sine of 30 degrees divided by one and that’s because the incident angle is 30 degrees and that's true for both the colors because they are in a single beam mixed together initially in the polystyrene, so they both have the same incident angle but the index of refraction for the two colors is different. It’s 1.493 in the case of green color and it’s 1.492 in the case of yellow and that’s the only difference between these two formulae and we end up with different angles. So, for green its 48.2881 degrees, is the angle of refraction and for yellow, it’s a little bit less 48.2451 degrees and so the difference in the angle is the difference between two numbers which is 0.043 degrees. Now, the next question is how far would the beam have to travel through air in order for the green and the yellow to be separated by one millimeter. So, this is delta x, the difference in the x-values for green and for ‘y’… and for yellow. So, x value meaning the amount they travel horizontally with respect to where they started. So, we are gonna take x g minus x y to find this delta x, and we’re gonna take the distance to be this hypotenuse of this triangle here. It’s not strictly clear whether they mean the distance traveled through air, meaning the hypotenuse which is what I think it means but they could also mean the distance from the surface. So, if this is the polystyrene there maybe what they are asking for is how far from the surface do the beams have to travel in order to be separated by a millimeter. So, in this case, this distance here, maybe that’s what they are asking for. I don’t really know so I am gonna give two answers to the question. So, well from this triangle we can see that sine of theta g, the angle of refraction for green is going to be the horizontal displacement of the beam x g divided by the hypotenuse d g and we are going to say the distance that the green travels on along this hypotenuse is approximately the same as for yellow. I mean clearly from this picture, they are not the same but the picture is not drawn to scale and so they are pretty much going to be same in reality because this is meant to be only one millimeter compared to a much much larger by many orders of magnitude distance along the hypotenuse. So, that’s an approximation that we have to make otherwise, we would have to solve using numerical methods or something. So, we’re gonna say that the distance… the green travels is the same as the distance the yellow travels. So, sine theta g equals the opposite x g over the hypotenuse d g and we will solve this for x g by multiplying both sides by d g and we have x g equals d g times sine theta g and for ‘y’ for yellow, it's essentially the same, except there's a different angle theta y and we will have x y as the opposite and then the hypotenuse is gonna be d y, but we are gonna approximate that to be the same as d g, as same as distance the green travels and so then in their delta x formula, we can substitute for the distance horizontally that the green travels and the horizontal distance that the yellow travels and this is a d g here and so we factor out the d g and then… and then you get d g times sine angle of refraction for green minus sine of the angle of refraction for yellow, approximately equals this one millimeter and then divide both sides by the bracket and you get the d g which is what we want to find the distance that the beams travel through the air in order to be separated by millimeter equals one millimeter divided by the sine of the theta g minus sine theta y. So, it's one millimeter divided by sine of 48.2881 degrees minus sine of 48.2451 degrees and that gives 2001.7 millimeters which is about two meters. So, this distance along the hypotenuse is three orders of magnitude more than the separation of one millimeter. So, that’s why the approximation of the green distance and the yellow distance being the same is acceptable. Now, what if they mean distance away from the surface? Well, if that’s the case then we can say that the cosine of theta g is the adjacent over the hypotenuse and we already found the hypotenuse. So, we can multiply both sides by the hypotenuse here and solve for the adjacent, which is this distance from the surface perpendicular distance. So, this distance from the surface is 2001.7 millimeters, length of the hypotenuse, times cosine of 48.2881 degrees which gives this many millimeters and we multiply it by one meter for every 1000 millimeter and we get 1.33 meters.