Question
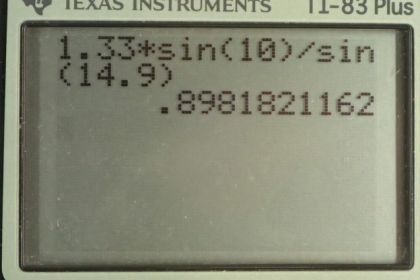
Suppose light travels from water to another substance, with an angle of incidence of and an angle of refraction of . (a) What is the index of refraction of the other substance? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- The index of refraction is greater than 1. This implies that the speed of light in the medium is greater than the speed of light in a vacuum. This is not possible.
- The angle is too large.
Solution video
OpenStax College Physics, Chapter 25, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A ray of light is travelling through water with an angle of incidence of ten degrees and then it counters a new material. It has an angle of refraction of 14.9 degrees. So, the first index of refraction is 1.33. And then, our question is what is the index of refraction of the second material? Well, Snell's law says that N one sine theta one equals N two sine theta two. So, we can solve for N two by dividing both sides by the sine of the angle of refraction. So, the index of refraction of the second material is index of refraction of the first material times sine of the incident angle divided by the sine of the refraction angle. So, that's 1.33 times sine of ten degrees divided by sine of 14.9 degrees, which is 0.898. Now, that is a problem because index of refraction always has to be more than or equal to one. But here, we have the index of refraction of the second material being less than one. Now, since index of refraction equals the speed of light in a vacuum divided by V, this implies that the speed of the light in this material is greater than the speed of light in a vacuum because V is C over N. You can solve for V by multiplying both sides by V over N here. With N less than one, V is going to be greater than C and that's not possible. So that means, this angle of refraction is probably too large. If this number was smaller, then sine of it would be smaller and by reducing the denominator, you can increase this quotient or increase N to a point where it's greater than one. There we go.