Question
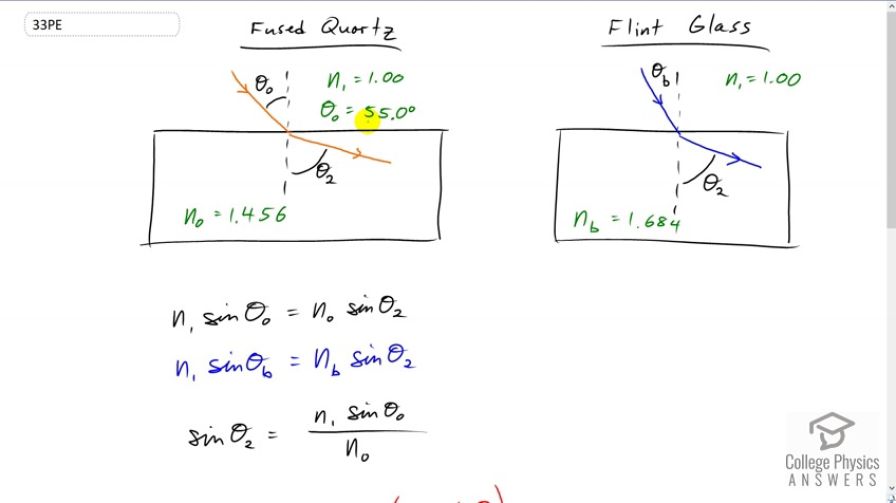
A ray of 610 nm light goes from air into fused quartz at an incident angle of . At what incident angle must 470 nm light enter flint glass to have the same angle of refraction?
Final Answer
Solution video
OpenStax College Physics, Chapter 25, Problem 33 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
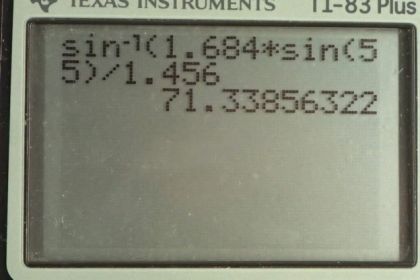
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Orange colored light with the wavelength of 600 nanometres is entering fused quartz at an incidence angle of 55 degrees and it has some angle of refraction and then consider a blue beam of light with a wavelength of 470 nanometres and it's entering flint glass and we want to figure out what incidence angle does it need in order to have the same angle of refraction that the orange did in fused quartz. So, we need to figure out what are the indexes of refraction for each of the colors in their respective materials. So, in fused quartz the color orange, it's index of refraction of 1.456 and in flint glass the color blue gets an index of refraction of 1.684. So, we will figure out an expression for sine theta two, given the fused quartz and the incident orange color and then we will substitute that into Snell’s law considering the blue incident beam. So, here is Snell’s law written down for each of these two different scenarios. So, we have the initial index of refraction which is just 1.00 in both cases because air doesn’t have very much dispersion meaning that the index of refraction is the same for all the different colors, 1.00 in each case. So we call that n one and then we have sine theta o for orange, that’s incident angle of the orange color equals the index of refraction that the orange color is experiencing. So, index of refraction for orange in fuses quartz in other words times sine of this angle theta two. Now, considering the blue light entering flint glass, we have the same sort of thing here except it's all to do with the blue color, although this is the same as it was for orange because we are told that the angle of refraction is meant to be the same for the blue color. So, we have index of refraction of blue in air which is just n one same as for orange in air, is sine of this incident angle that we have to find for the blue color and that equals the index of refraction that blue experiences in flint glass times sine of the index or the angle of refraction theta two. So, if we re-arrange this formula to solve for sine theta two, we divide both sides by n o and we get this expression, which we can then substitute in for sine theta two in our Snell’s law for the blue color going into flint glass. Yep. So, we have written Snell’s law for the blue colour but I have substituted n one sine theta orange divided by n orange in place of sine theta two and then we take a… the inverse sine of both sides after dividing both sides by n one in which case it cancels and then we take the inverse sine on both sides to solve for theta b. So, the angle of incident, that the blue needs in flint glass is the inverse sine of n b sine theta o divided by n o. So, it's inverse sine of 1.684, the index of refraction of color blue in flint glass times sine of 55.0 degrees which was the given incident angle for the orange going into fused quartz divided by the index of refraction of orange in fused quartz of 1.456 and this gives an angle of 71.3 degrees.