Question
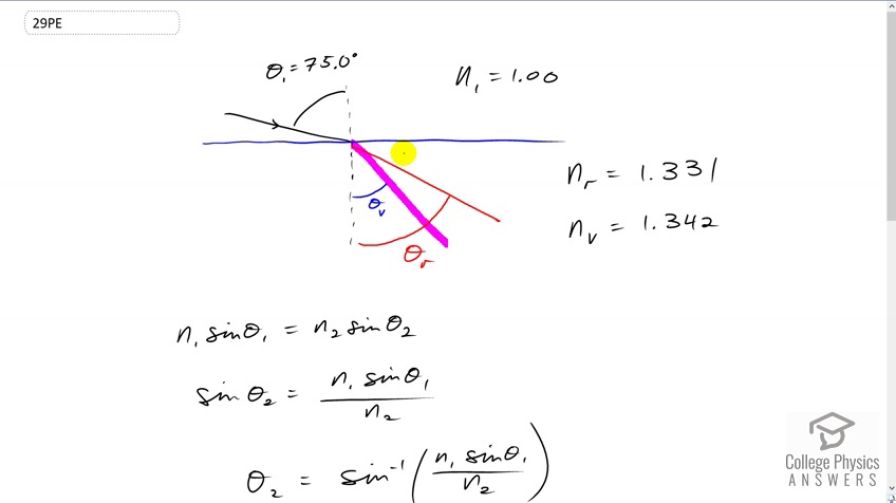
A beam of white light goes from air into water at an incident angle of . At what angles are the red (660 nm) and violet (410 nm) parts of the light refracted?
Final Answer
Solution video
OpenStax College Physics, Chapter 25, Problem 29 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
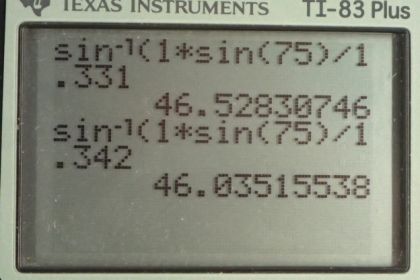
This is College Physics Answers with Shaun Dychko. Some white light is incident at an angle of 45 degrees on the surface of this water. And, some of the red light will be refracted at such and such an angle, we'll call it theta r. And the violet part of this white light beam will be refracted at a different angle, we'll call that theta v, for violet. And this happens because the index of refraction of water is different for different wavelengths, for different colors. And this is responsible for dispersion, lots of materials are like this; their indices of refraction — even though at table 25.1 gives the impression that the index of refraction is a property of the material and is only one number, that's not true: there's a different number for every color in each material. So, we're going to figure out the angle of refraction for the red color and then do it again for the violet color. Now, Snell's law says that the index of refraction of the initial medium times sine of the angle of incidence equals the index of refraction of the second medium times sine of the angle of refraction. And we can solve for theta two by dividing both sides by n two. And then, take the inverse sine of all this, and you get that the angle of refraction is the inverse sine n one times sin theta one over n two. Now, the numbers that we plug in here are gonna be different depending on what color we're considering. So we'll consider the angle of refraction for red color. That's gonna be the inverse sine of n one times sin theta one over the index of refraction of water for the color red. And so that's the inverse sine of one times sin 75 degrees divided by 1.331. And that gives an angle of refraction for red of 46.5 degrees. Now in the case of violet, the index of refraction for the color violet in air is the same as the index of refraction for the color red in air. So air is like that, it does not have much dispersion. It does not change its index of refraction for different colors very much. But water, on the other hand, has a significantly different index of refraction for the color violet than it did for the color red. So we have for violet, it's the inverse sine of one times sine of 75 divided by 1.342, he index of refraction for violet in water. And this gives an angle of refraction of 46.0 degrees.