Question
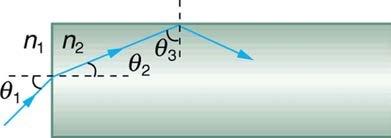
A light ray entering an optical fiber surrounded by air is first refracted and then reflected as shown in Figure 25.56. Show that if the fiber is made from crown glass, any incident ray will be totally internally reflected.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 25, Problem 27 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
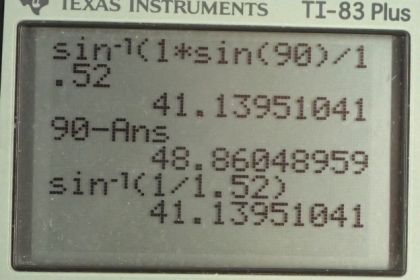
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have an optical fiber made out of crown glass and it's surrounded by air. So that means n one is 1.00 and the index of refraction of the fiber is 1.52. And we're going to show that no matter what the angle of incidence is here, theta one, there will always be total internal reflection of any ray inside this fiber. So, we're going to figure out what is the minimum theta three that's possible. And then, we'll also calculate the critical angle for the crown glass-air interface and show that this theta three is always going to be greater than the critical angle. And since that's the case, there will always be total internal reflection. So, let's find the smallest theta three that's possible though. Because the smaller this angle of incidence here, the better chance it has of going through the interface. So, there is an angle small enough such that this ray will go through, but we'll show that theta three will never get that small. Okay. So, theta three plus theta two, this angle here, add up to 90 because they're part of this triangle here, which is a right triangle. And, you know, the total angles inside a triangle is 180. And then this ones 90 though, so that means 90's left over for theta two and theta three. In which case, theta three is 90 minus theta two when you subtract theta two from both sides. Now we want to get the minimum possible theta three, and that will occur when you have the maximum possible theta two. So, let's figure out what the maximum possible theta two is. Now, we're going to turn our attention to this interface here, and we'll use Snell's law and show what the maximum theta two is based on the maximum theta one. And we can control theta one; that's when it's maximum, it's gonna be 90 degrees. I mean, strictly speaking, at 90 degrees, it's not going to enter the fiber at all, but, you know, that's the border between when it does and doesn't. So, we're gonna take theta one to be 90 degrees... and... which we do down here. And we're gonna use Snell's law to figure out what theta two will be at its maximum. So, Snell's law says the index of refraction of the first medium, which is air, times sine of the angle of incidence theta one, equals n two sine theta two. And we'll solve for theta two by dividing both sides by n two. And then, take the inverse sine of both sides. So theta two is the inverse sine of n one sin theta one over n two. Now, theta two maximum is gonna be the inverse sine of n one times sine theta one maximum. And that's where I talked about having theta one being 90 degrees. And then we plug in numbers here. So it's the inverse sine of index of refraction of air, times the maximum possible angle of incidence from the air, which is 90 degrees, divided by the index of refraction of the crown glass, which is 1.52, giving a maximum theta two 41.1395 degrees. So that means theta three minimum is 90 minus that theta two maximum, which is 48.86 degrees. So now, we're going to see how this compares with the critical angle. Now, we need to consider this interface here now and we have the index of refraction of the medium we're starting in, which is crown glass, times sine of the critical angle, equals the index of refraction that we're going to, which is air, times sine of the angle of refraction at the critical angle. So when we have whatever the critical angle is here, the angle of refraction is going to be 90. So we can solve for theta c then. It's the inverse sine of the second medium, which is air, which has an index of refraction of one, times sine of 90, divided by 1.52, which is 41.1395 degrees. And we can see that this maximum... or this minimum, sorry, possible theta three is always going to be greater than this number. So, because theta three will always be more than the critical angle, there will always be total internal reflection.