Question
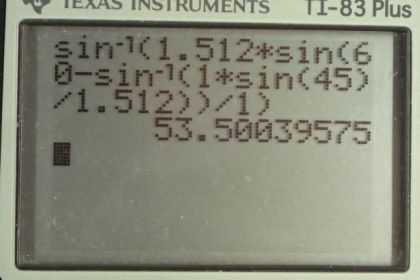
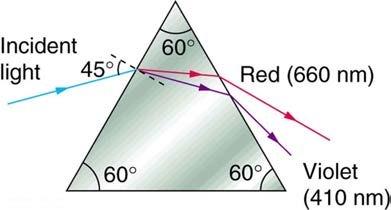
A narrow beam of white light enters a prism made of crown glass at a incident angle, as shown in Figure 25.57. At what angles, and , do the red (660 nm) and violet (410 nm) components of the light emerge from the prism?
Final Answer
Solution video
OpenStax College Physics, Chapter 25, Problem 35 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An incident beam of light consisting of red and violet colors mixed together hits this interface here with this crown glass prism at an angle of 45 degrees and there is a difference in how the red and the violet are refracted because they experience different indexes of refraction. So, in crown glass red experiences an index of refraction of 1.512 and for violet it’s 1.530. So, that difference in index of refraction causes a difference in the angle of refraction and we want to figure out what is this angle for violet and what is this angle for red when it comes out the other side of this triangular prism. So, we will take this problem step by step by first of all considering this interface here where the light first enters the prism. So, that’s this line here and we are given this 45 degrees angle and we will figure out this angle of refraction alpha r, this angle between the normal and… and the beam as it travels inside the prism. So, Snell’s law is that n one sine theta one, that’s the index of refraction in first medium which is air equals… or times sine of the angle of incidence theta one equals the index of refraction in crown glass and if we consider the color red let’s put a subscript ‘r’ in each of these things times sine of the angle of refraction, we call it alpha r here and then we can solve for alpha r by dividing both sides by n r and then taking the inverse sine on both sides. So, this tells us this angle alpha, the inverse sine of n one sine theta one over n r and n one is going to be the same for both red and violet because air has index of refraction of 1.00 for all the different visible colors. Now, inside this prism we can think of a triangle like this. We are going to figure out what beta is using some geometry here. This is beta z, the angle of incidence as the beam hits this exit surface of the prism And... and we know what the angles are here and here because these dotted lines are normal to the surfaces and so by definition these are 90 degrees each and the four angles inside a quadrilateral have to add up to 360. So, since we have two 90 degrees angle here in green, that accounts for 180 leaving a 180 left over to share between this angle here and this one at the bottom corner and we are given this one 60 at the top and that leaves 120 at the bottom. So that’s useful because then we can figure out what beta is. beta for… is going to be 180, which is the interior angles of a triangle minus the 120 we just figured out minus this anglealpha and if we are considering the color red then we put a subscript ‘r’ for alpha r and we are finding beta r and 180 minus 120 is 60. So, angle beta is gonna be 60 minus the angle alpha. Okay, and now we are gonna be considering this exit surface and we have this incident angle of beta and then the angle of refraction is our final answer theta. So, the index of refraction of the first medium which we put a subscript ‘r’ on for the index of refraction of red in crown glass times sine of this angle beta equals n one again because that’s the index of refraction outside the prism in air times sine theta r. I guess this would need an ‘r’ as well if we just considering red and we can solve for the angle by dividing both sides by n one and taking the inverse sine on both sides. Now, this beta r we'll have to substitute with something else, we figured out before that it equals 60 minus the angle alpha. So, for red it’s gonna be 60 minus alpha r and then alpha r we figured out back here, is the inverse sine of n one sine theta one over n r and so we substitute that for here in place of alpha r and now we have a formula that we can plug numbers into to get our final answer. So, the angle that the red color exits the triangular prism is the inverse sign of 1.512 which is index of refraction of red in crown glass times sine of 60 degrees minus the inverse sign of one times sine 45, which was the incident angle, divided by 1.512, all divided by one, the index of refraction of red in air and that gives 53.5 degrees. So, the red color will exit at 53.5 degrees with respect to normal of the exit surface. Then violet is going to have a higher angle we expect because the index of refraction is higher for violet and so we expect it to bend more and so it’s going to be deviating more from this normal here and then we plug in numbers to verify that that’s true. So, it’s gonna be the inverse sine of index of refraction of the color violet in crown glass times sine of 60 minus inverse sine one times sine 45 degrees incident angle divided by 1.530, all over one giving an angle of 55.2 degrees. So, theta violet is 55.2 degrees.