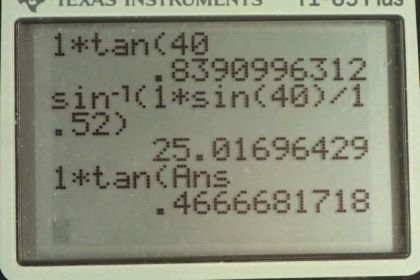
Question
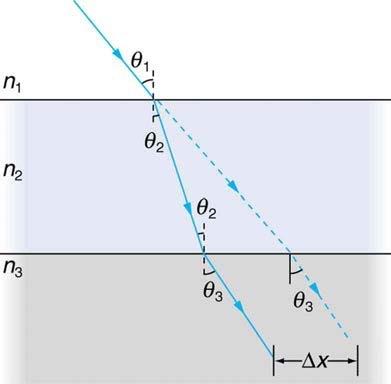
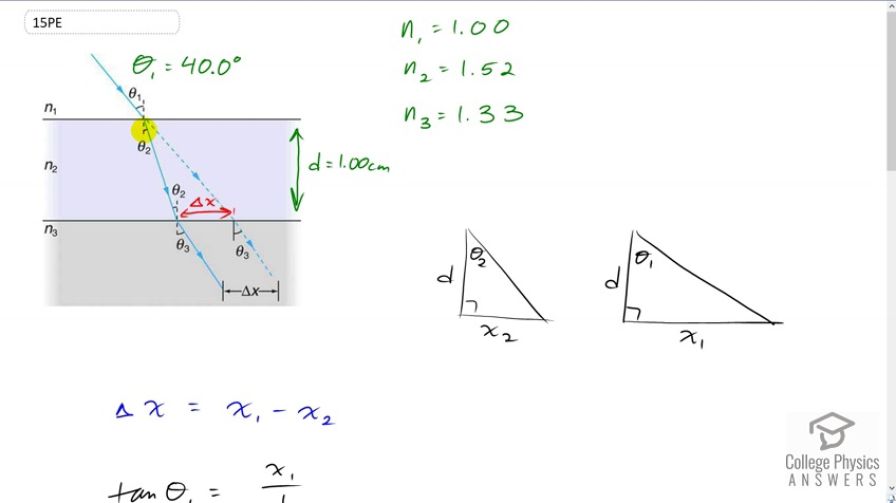
Suppose Figure 25.54 represents a ray of light going from air through crown glass into water, such as going into a fish tank. Calculate the amount the ray is displaced by the glass (), given that the incident angle is and the glass is 1.00 cm thick.
Final Answer
Solution video
OpenStax College Physics, Chapter 25, Problem 15 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A ray of light is travelling through air and then goes through a pane of glass around an aquarium and then enters some water. This glass is crown glass with an index of refraction of 1.52. Index refraction for air is 1.00 and that of water is 1.33, although it turns out that the water part is not going to matter. This Delta X, the amount of displacement of the ray as a result of going through this glass should actually be drawn here. We're going to draw it here. So, we're going to figure out what this distance is. Now, we can consider two different triangles. This triangle in yellow here represents this triangle here. And, a calculated distance X one. That's from here to where the ray would be, this is all here. This is where the ray would be if there had been no refraction. In other words, if there had been no crown glass here. And then, this triangle in blue represents what's actually happening with the presence of the glass and I've drawn, that's this drawing here. And so, the Delta X is displacement due to the refraction through the crown glass is going to be X one minus X two. Okay. So, let's figure out X one first, that's the easy part. We can say that the tangent of theta one equals the opposite X one divided by the adjacent, which is the thickness of the glass D, or as we're told is one centimeter. And so, that means X one is D times ten theta one. So, that's one centimeter times tangent of 40 degrees, because we're told that the angle of incidence is 40 degrees here, theta one. And, this works out to 0.8391 centimeters. Now, let's next consider what X two is. Well, it's going to have a different angle theta two and we'll use Snell's law to figure out what that theta two should be. And, for the same reason as this triangle, X two is the thickness of the glass multiplied by tangent of that angle theta, but in this case it's theta two. So, Snell's law says the index of refraction of the first medium, which is air, times sine theta one, which is 40 degrees, equals the index of refraction of the second medium, which is crown glass times sine of the angle of refraction, theta two. And so, we divide both sides by N two and we get sine theta two is N one sine theta one over N two. And, that gives us theta two is the inverse sine of all of this. So, that's the inverse sine of 1.00 times sine 40 divided by the index of refraction of crown glass, which is 1.52, giving an angle of 25.02 degrees. So, we plug that in for theta two in our formula for X two. And so, X two is one centimeter times tangent of 25.02 degrees, giving 0.4667 centimeters. And so, the Delta X then is the distance if there was no refraction, X one, 0.8391 centimeters, minus this distance that we have with refraction 0.4667 centimeters giving a total change of 0.372 centimeters, which we'll express in millimeters by multiplying by ten millimeters per centimeter. And so, it's going to be displaced 3.72 millimeters.