Question
What is the best coefficient of performance possible for a hypothetical refrigerator that could make liquid nitrogen at and has heat transfer to the environment at ?
Final Answer
Solution video
OpenStax College Physics, Chapter 15, Problem 39 (Problems & Exercises)
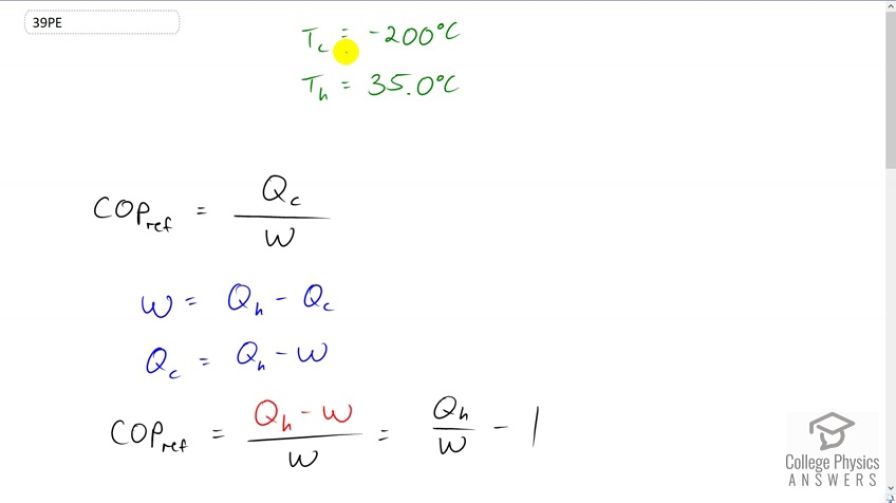
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the maximum possible coefficient of performance for a refrigerator that's making liquid nitrogen and the cold temperature is going to be minus 200 degrees Celsius. And, the refrigerator is operating in an environment that is at 35 degrees Celsius, so it's expelling heat into a high temperature reservoir at 35 degrees Celsius. So, the coefficient of performance for a refrigerator is the amount of heat that is drawn out of the cold temperature reservoir divided by the amount of energy needed to make that heat transfer happen. So, this is electrical energy in this case. And, they call the W or work energy needed to make the heat pump operate. Now, we need to express this formula in terms of Qh, the amount of heat delivered to the high temperature reservoir because we have an efficiency formula and efficiency is considered the work done divided by Qh. And so, we need to have Qh up here in our coefficient of performance formula in order to substitute in efficiency, and then we can replace efficiency with Carnot efficiency, 1 minus Tc over Th. So, that is the reason why we are doing these steps here. So, we're going to replace Qc with Qh minus W because we know that the work done by a heat pump is the difference between the heat taken from or delivered to, I guess in this case, delivered to the high temperature reservoir minus the heat drawn from the cold temperature reservoir. And so, we'll solve this for Qc and we'll add Qc to both sides and subtract W from both sides. And then, this works out to Qc equals Qh minus W. So, we replace Qc with that and then divide both terms in the numerator by this W in the denominator, and we get Qh over W minus 1. Now, efficiency is W over Qh. Normally, it's considered the work done by a heat engine divided by the heat drawn from high temperature reservoir. So, we can see that this is the reciprocal of that, and so we can replace Qh over W with efficiency to the power of negative 1, exponent negative 1 being the reciprocal. And, efficiency, since we want to know the theoretical maximum coefficient of performance, we will take the theoretical maximum efficiency, which is called the Carnot efficiency, and that's 1 minus the cold reservoir temperature divided by the hot reservoir temperature. And so, we replace this efficiency with 1 minus Tc over Th. And so, all this is to the negative 1 minus 1. This is the theoretical maximum coefficient of performance for a refrigerator. And, we can get a common denominator here by multiplying this 1 by Th over Th, and this makes Th minus Tc all over Th, and now it's a single fraction that we can then flip in order to deal with this exponent negative 1. So, that's Th over Th minus Tc minus 1. And then, again, we'll get a common denominator by multiplying this 1 by Th minus Tc over Th minus Tc. And, we end up with Th minus Th minus Tc in brackets divided by Th minus Tc. And then, distributing this minus sign into the brackets gives a negative Th and then a positive Tc and then this Th and this Th makes zero. And so, we have Tc over Th minus Tc. So, that is the formula for the maximum theoretical coefficient of performance for a refrigerator. And now, we can plug in numbers into it. So, we have minus 200 degrees Celsius converted into Kelvin by adding 273.15 and divide by the high temperature which is 35 degrees Celsius minus the cold temperature of negative 200 degrees Celsius. And, notice that I did not bother converting these to Kelvin. I could have, and it would have been fine. But, since we're taking a difference between temperatures, adding 273 to each of them would make no difference, so to speak. But, this temperature on the top does need to have the 273 added to it because this is division. Okay. So, it works out to 0.311 is the best possible coefficient of performance for a refrigerator making liquid nitrogen.
