Question
A large electrical power station generates 1000 MW of electricity with an efficiency of 35.0%. (a) Calculate the heat transfer to the power station, , in one day. (b) How much heat transfer occurs to the environment in one day? (c) If
the heat transfer in the cooling towers is from water into the local air mass, which increases in temperature from to , what is the total increase in entropy due to this heat transfer? (d) How much energy becomes unavailable to do work because of this increase in entropy, assuming an lowest temperature? (Part of could be utilized to operate heat engines or for simply heating the surroundings, but it rarely is.)
Final Answer
Solution video
OpenStax College Physics, Chapter 15, Problem 55 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
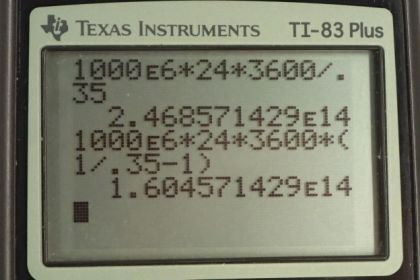
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A power plant has a power output of 1000 megawatts which is 1000 times tenth to the six watts with an efficiency of 0.35. Now we want to figure out how much heat is input into this power plant. In other words how much heat is consumed by burning fossil fuels. So we have the efficiency is the energy output divided by the amount of heat consumed and the amount of heat consumed we can write as W over efficiency. This is what we're solving for Qh. So we will multiply by Qh over efficiency on both sides. And we have this formula here Qh equals W over efficiency and we don't know what W is though, but we can figure it out by using this expression for power. So power output is the work output or the energy that has been output by the power station divided by time and will solve this for W by multiplying both sides by t. Hence, we have the work is power multiply by time and so we'll substitute that in place of W in our formula here. So the amount of heat that is consumed from the high temperature reservoir is power times time divided by efficiency. And so we told to consider one full day here to calculate the heat transfer to the power station in one day. So a day is this many seconds, we have to convert this time unit into seconds by multiplying by 24 hours per day then times by 3600 seconds per hour. And so we multiply that by the 1000 megawatts and we divide by a 0.35 efficiency and we get 2.47 times tenth to the 14 joules. So, this is the amount of heat energy released by burning the fossil fuels. Then in part b, we're asked how much heat is released to the environment and that's going to be the amount of heat released by burning the fossil fuels minus the amount of energy that goes into the useful end product which is electrical energy. And so we also have this expression for work is the difference between the heat-in minus the heat-out and we rearranged it of Qc. Now Qh is power times time divided by efficiency. That's what we've found here and work is power times time. So we have Pt over efficiency minus Pt and we factor Pt out. And it's Pt times one over efficiency minus one and then we can plug in numbers. So it's 1000 megawatts times one day converted into second times one over 0.35 minus one which is 1.6 times tenth to the 14 joules of energy wasted and released to the cold temperature reservoir released to the environment. Now what is the total change in entropy is the next question. So there is change in entropy in the cooling towers and there's also change in entropy of the air to which this heat is being released. Now the cooling towers they're losing heat and the heat is going into the air. And so when we substitute for change in entropy here we're gonna have a negative Q and negative representing the fact that the cooling tower is having heat taken out of it and for the air it's gonna be positive Q because that's where the heat is going and this numerator is meant to be the amount of heat put into the system and so air is gaining. So it's gonna be positive Q. Now we divide by the temperature and for the cooling tower that's a constant 35 degrees Celsius for the air. However it's changing from 18 to 20 degrees Celsius. And so we're gonna simplify this by taking the average temperature. We can factor the common factor Q out and so we have Q times one over average air temperature minus one over cooling tower temperature and that is 1.60457 times ten to the 14 joules. This is the amount of energy expelled to the environment and times one over average temperature of the air. So 18 plus 20 over two converted into Kelvin by adding 273.15 minus one over 35 degrees Celsius converted into Kelvin and we get 2.85 times ten to the ten joules per Kelvin is the total change in entropy. Now the amount of work energy that is unavailable to do any work now is this change in entropy multiplied by the lowest temperature in our system. So that's 2.8517 times tenth to the 10 joules per Kelvin times 18 degrees Celsius which is the low temperature of the air plus 273.15 to convert into Kelvin and this gives 8.30 times tenth to the 12 joules of energy is unavailable to do work.