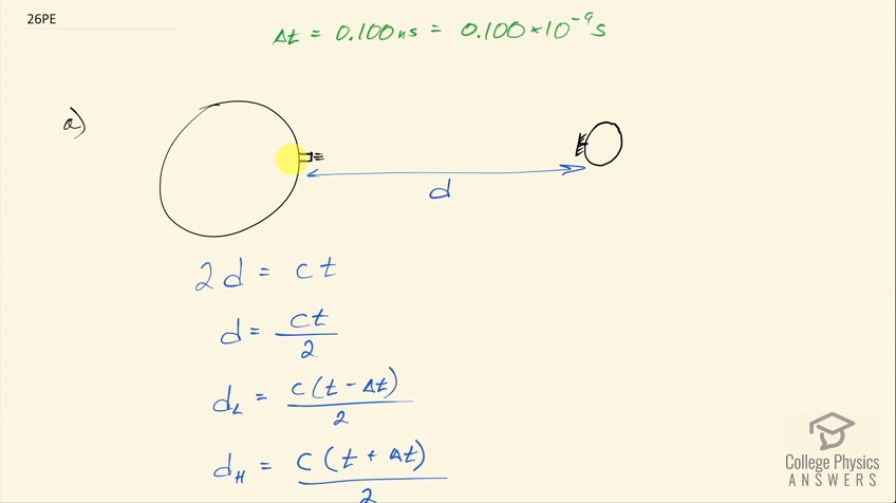
Question
Lunar astronauts placed a reflector on the Moon’s surface, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. (a) To what accuracy in meters can the distance to the Moon be determined, if this time can be measured to 0.100 ns? (b) What percent accuracy is this, given the average distance to the Moon is ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 24, Problem 26 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Astronauts have installed a mirror on the Moon that is used to reflect a laser being projected from the Earth and the round trip time that this light takes to get from the Earth to the Moon and back is used to figure out the distance to the Moon. So 2 times this distance between the Earth and the Moon is equal to the speed of light multiplied by the time because the time represents two trips— a round trip or traversing this distance twice—once to the Moon and then again back so that's why we have the number 2 there... 2 times the Earth-Moon distance. So we can solve for d by dividing both sides by 2 and so d is the speed of light times the total time divided by 2. Now we have some error in our time measurement— we are told—of 0.100 nanoseconds, which is 0.100 times 10 to the minus 9 seconds and the question is what is the error then in this distance measurement? So the lowest possible distance will be c times the time measured minus the error over 2 and the high end of the distance range that's possible is c times the time plus the error divided by 2. So that gives an error in the distance equal to half of this difference between the high and the low because this Δt is a plus or a minus so the time then is some number plus or minus this error Δt and so this Δt is spread about the number equally and so if you have this the maximum possible time minus the minimum possible time that will be Δt times 2 because if you have some number and you go this distance to the right by adding Δt and this distance to the left by subtracting Δt... I'm imagining a number line here this difference between the lowest and the highest this being t low and this being t high this difference consists of 2 times Δt. Okay! And then you know take the same picture and think of distance low and distance high and so anyway... we have to divide this difference between the two extremes by 2 to get the error in the distance. So plug in our formula for the high estimate for the distance and then minus the low and then we are still dividing that by 2 or in other words, multiplying by a half this works out to one-quarter when you factor out the one-half from both terms and then multiply by the one-half outside the brackets so one-quarter times ct plus cΔt minus ct plus cΔt— this minus and this minus making a plus here. So ct minus ct is zero and we have one-quarter times 2cΔt which is cΔt over 2. Then we plug in the speed of light 2.998 times 10 to the 8 meters per second times 0.100 times 10 to the minus 9 seconds is our error in time divided by 2, this works out to 1.50 centimeters which is an amazingly precise measurement. And the percent error is this error divided by the distance itself times 100 percent so that's 0.01499 meters divided by the distance between the Earth and the Moon of 3.84 times 10 to the 8 meters times 100 percent and that is 3.9 times 10 to the minus 9 percent error.
