Question
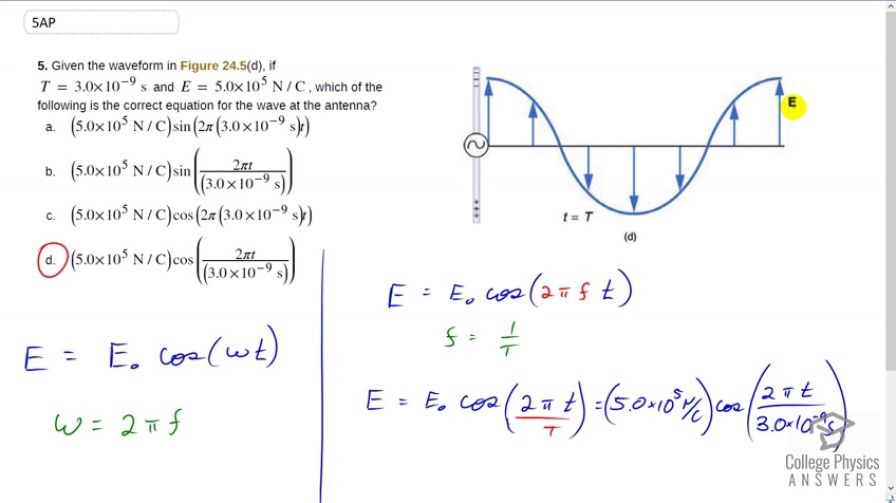
Given the waveform in Figure 24.5(d), if and , which of the following is the correct equation for the wave at the antenna?
Final Answer
(d)
Solution video
OpenStax College Physics for AP® Courses, Chapter 24, Problem 5 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. So we have this picture which is Figure 24.5 Part D and it has electric field strength on the vertical axis and time on the horizontal axis and we've plotted one full period. And the question is, which equation here, correctly describes this picture? Now we know it has to have cosine because cosine of zero, we will take this to be zero here, is at its maximum and so cosine of 0 is 1. And so this maximum here is going to be corresponding to cosine so we can exclude options A or B. And then we have to see that the amplitude is this; 5 times 10 to the 5 newtons per Coulomb which doesn't really help because both C and D both have that. So we need to consider this formula for the electric field is the peak times cosine of the angular frequency multiplied by time and the angular frequency is 2 Pi times frequency which we can then substitute in. Frequency is 1 over period and we are given periods. So this could be useful. And so we can substitute that in and so we have 1 over T there in place of F and so E naught is 5 times 10 to the 5 newtons per Coulomb and we have cosine of 2 Pi times time divided by 3 times 10 to the minus 9 seconds period. And so that is corresponding to this option here D.