Question
A 4-ton air conditioner removes (48,000
British thermal units) from a cold environment in 1.00 h. (a) What energy input in joules is necessary to do this if the air conditioner has an energy efficiency rating (EER) of 12.0? (b) What is the cost of doing this if the work costs 10.0 cents
per (one kilowatt-hour)? (c) Discuss whether this cost seems realistic. Note that the energy efficiency rating (EER) of an air conditioner or refrigerator is defined to be the number of British thermal units of heat transfer from a cold environment per hour divided by the watts of power input.
Final Answer
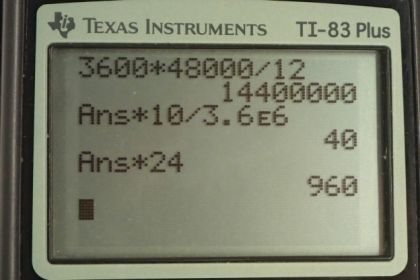
- 40.0 cents
- This is realistic since it costs $9.60/day
Solution video
OpenStax College Physics, Chapter 15, Problem 45 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An air conditioner has an energy efficiency rating of 12. And the formula for energy efficiency rating is a bit strange because the units are unusual. So the Qc represents the amount of heat taken out of the cold temperature reservoir. And it's in units of British Thermal Units or btu for short. And this time here that it's divided by is in hours. And this time, and this time, are the same amount of time, but the units are different. And so, our time is one hour that we're given in our question because it says: "The air conditioner removes 5.06 times 10 to the seven Joules, or 48000 btu in one hour." So the time is one hour, and we're going to write one hour for t1. And then for t2, we write one hour as well but we use units of seconds. So that's 3600 seconds. And W is going to be energy in Joules. Okay, so we want to figure out what W is: the amount of energy that will be consumed in order to transfer this much heat. And so, we'll multiply both sides by W over t2. And also divide both sides by one over energy efficiency rating. And then also, multiply this side by W over t2. And, we end up with W over t2 equals Qc over t1, divided by energy efficiency rating. And then we'll multiply both sides by t2. So, the amount of work energy needed to run this air conditioner is gonna be the time, multiplied by the heat transferred, divided by, per hour so divided by t1, divided by the energy efficiency rating. So that's 3600 seconds, times 48000 btu per hour, divided by 12 btu per one hour, which is the energy efficiency rating. And this works out to 1.44 times 10 to the 7 Joules. Now, the cost to run this air conditioner is going to be that energy consumed multiplied by 10 cents, for every 3.6 times 10 to the six Joules, which works out to 40 cents. So it's using 40 cents per hour or .4 dollars per hour. And to see if this is realistic, let's multiply that by 24 hours per day, if we assume that it's running every hour which it probably wouldn't be because, you know, there's a thermostat, and it would stop running once it gets to a proper set temperature. Anyway, this works out to nine dollars and sixty cents per day, in a worst case scenario where it's operating all the time. And that is a reasonable amount of money. And there we go.