Question
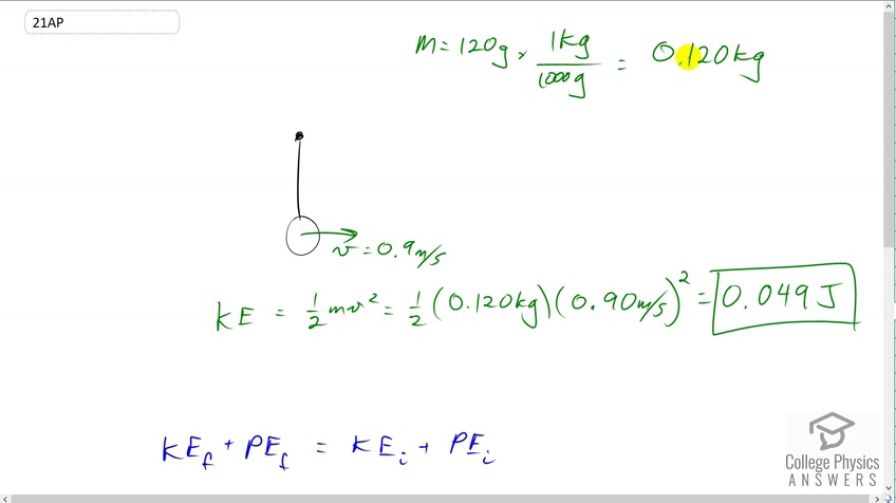
You have a 120-g yo-yo that you are swinging at 0.9 m/s. How much energy does it have? How high can it get above the lowest point of the swing without your doing any additional work, on Earth? How high could it get on the Moon, where gravity is 1/6 Earth’s?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 7, Problem 21 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This yo-yo is at the bottom of its swing with a speed of 0.9 meters per second. It has a mass of 120 grams which is 0.120 kilograms. We're asked to find its energy which is kinetic energy, so it's one half mass times speed squared. So that's one half times 0.12 kilograms times 0.9 meters per second squared, which is 0.049 Joules. Now, its final mechanical energy is going to equal its total initial kinetic energy or mechanical energy I should say. So in the final case when it's at the very top of its swing up here, it'll have no kinetic energy because we're looking for the case where it's just barely able to get up there. So this'll be the highest height it can possibly get. It'll be the height where all of its energy that it has here, is converted entirely into potential energy to reach its maximum possible height. Initially it has no potential energy because we'll take this to be a reference level. So that means m g, maximum height equals one half mass times speed at the bottom squared. The m's cancel and we can divide both sides by g and this gives the height is the speed squared divided by two, times gravitational field strength. So that's 0.9 meters per second squared divided by two times 9.8 meters per second squared and that gives about 4.1 centimeters is the maximum height on earth. Now, on the moon the formula is the same form but the number for substituting for the acceleration due to gravity will be different. We're told that it is one-sixth that of earth. So I've substituted 9.8 meters per second squared divided by six here. We end up with 25 centimeters is how high the yo-yo could go on the moon.
