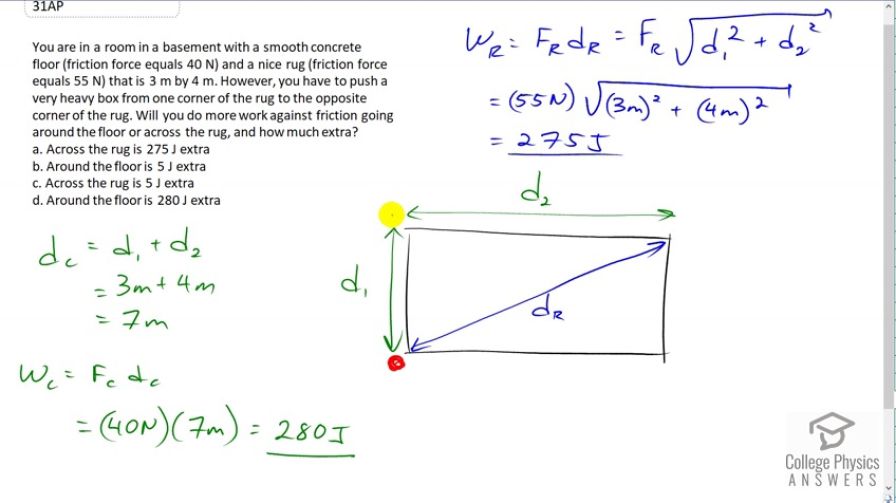
You are in a room in a basement with a smooth concrete floor (friction force equals 40 N) and a nice rug (friction force equals 55 N) that is 3 m by 4 m. However, you have to push a very heavy box from one corner of the rug to the opposite corner of the rug. Will you do more work against friction going around the floor or across the rug, and how much extra?
(a) Across the rug is 275 J extra
(b) Around the floor is 5 J extra
(c) Across the rug is 5 J extra
(d) Around the floor is 280 J extra

Video Transcript

This is College Physics Answers with Shaun Dychko. So the box begins in this corner of the rug and the options are to move it along the smooth concrete this distance d one and then again along distance d two to get to this position, or we can move it with -- by pushing it with a greater force across the rough rug but go the shorter distance which is the hypotenuse directly from corner to corner. So let's consider the case across the concrete first of all. So the total distance traveled would be d one plus d two. So that's three meters plus four meters which is seven meters and the work done to push along the concrete would be the force applied on the concrete which is 14 newtons, times the total distance on the concrete, seven meters, for a total of 280 joules. Then for the case where we go across the rug, we're going to push with this force, the rug force which is 55 newtons multiplied by this distance across the rug which is the square root of d one squared plus d two squared. So that's 55 newtons times square root of three squared plus four squared which gives 275 joules. So it turns out that there is less work to go across the rug, or I guess to put it in terms that work with these options here, we should say that across the floor is 5 joules extra compared to the rug. So option B is the answer.