Question
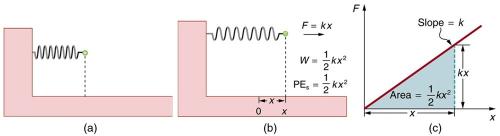
Look at Figure 7.10(c). You compress a spring by , and then release it. Next you compress the spring by . How much more work did you do the second time than the first?
- Half as much
- The same
- Twice as much
- Four times as much
Final Answer
(d)
Solution video
OpenStax College Physics for AP® Courses, Chapter 7, Problem 3 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. In figure 7.10 part C, you can see a graph showing the force applied versus the amount of compression of the spring and the work that this force does is the area underneath this curve. So the area is this triangle and so given a compression of distance x, the area is going to be one half times kx being the height and that comes from this force formula, Hooks Law. I mean this negative sign there I suppose that just has to do with direction and we care only about magnitude here. So the magnitude of this height is kx and the base of this triangle is x. Then if you were to compress it by two times that distance -- let's draw that. We'll take something that is this length and we'll move it over here and so now the base of the triangle will be at this point. Then we'll go up to the point where it intersects this line here -- there, and so now we have a distance of 2x on the base and the height as well k, times 2x as well. But what we care about is the graphical interpretation of this and that is -- let's consider how much area is underneath this curve now. Well, if you had this triangle -- here is the area that we had before. If we move that triangle over here we can see that this new area is more than two times the old triangle because this new area which is in purple is the work done. If you consider the old area, the work done previously with a compression of one x, it equals this -- I guess I should try a different color -- it equals this green triangle and then two times the green triangle would be that green triangle plus that green triangle again here and you can see that two times the area before does not fill up the entire area under the curve when the spring is compressed twice what it was before. So this is just a way of illustrating that the work done is non-linear. The work done when you compress by twox is not two times the work done when you compress by a single x because in green, I've shaded the total area one would expect with two times the work done in the first case and it's not accounting for all the area. It's missing this portion here and that portion there -- well, if we were to take this triangle and it's a bit complicated to do, but if we were to reflect it, it would fill up this area and then this bit here would be of equal size to that triangle yet again. So there are one, two, three, four triangles fitting into this total space under the curve when you compress by 2x. So, the amount of work done in this case where you compress by 2x is four times as much as before. The answer is D.