Question
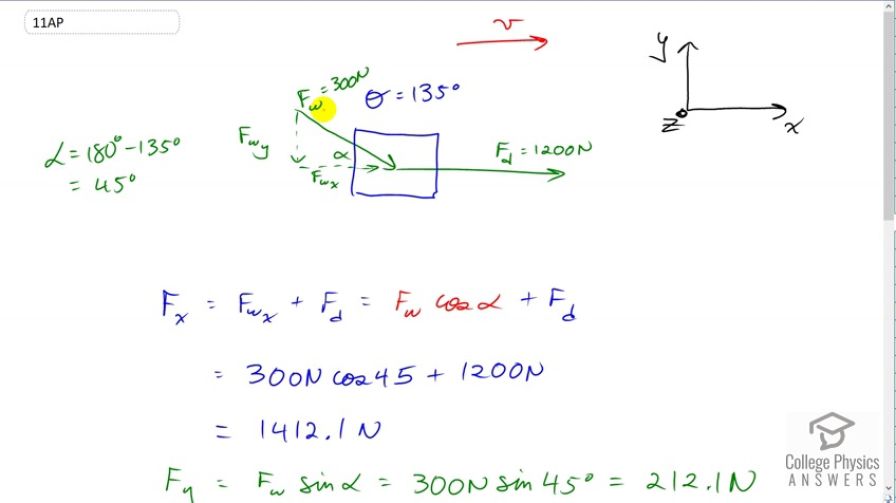
You are participating in the Iditarod, and your sled dogs are pulling you across a frozen lake with a force of 1200 N while a 300 N wind is blowing at you at 135 degrees from your direction of travel. What is the net force, and will your kinetic energy increase or decrease?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 7, Problem 11 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
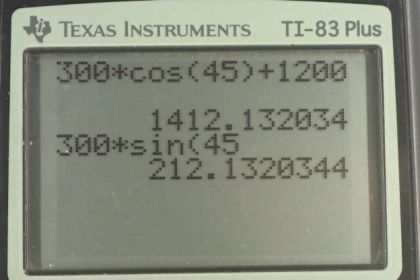
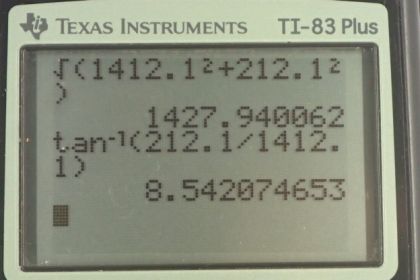
This is College Physics Answers with Shaun Dychko. This dog sled is being pulled by some dogs with a force of 1200 newtons in the direction of travel and there is a wind blowing at an angle of 135 degrees with respect to the direction of travel. This wind is in the plane of the ground and so there is a component of it pushing in the direction of travel and there is a component pushing downwards not into the ground but along the ground just you know, if this was pushing to the west then this would be pushing -- or this was pushing east say, this would be pushing south. Okay. So we're going to find the net force by finding the, well, the components in the x and y direction first and then take the square root of the sum of the squares of each component. So in the x direction we have the dog sled force plus the x component of the wind and that's going to be the force of the wind, times cosine of this angle alpha in here. This angle here is 180 minus 135 so that makes 45 degrees. So we have 300 times cos 45 plus 1200 makes 1412.1 newtons, the force in the x direction. By the way, I drew my coordinate system here with the letter z with the arrow coming out of the page just so that you know that when this is pointing down like this, this doesn't mean down into the ground. Instead it means down in the plane of the ground. So this is not digging a hole. This is instead just going to the south and this is going to the east. Okay. The y component is the force of the wind multiplied by the sine of alpha because this is the opposite leg of this green triangle. We have 300 times sine 45 which is 212.1 newtons. Then to find the magnitude of the net force, take the square root of each of those components squared. So that's the square root of 1412.1 squared, plus 212.1 squared, giving us 1430 newtons. The angle of this net force, let's call that gamma, so the net force is going to be something like, something like this, where you have this F wx tacked on to the end there and then you have the y component F wy. So this line here is the net force and right now we're finding this angle gamma which is not alpha by the way, not the same as alpha. These are not opposite angles. Okay. By the way, these are not opposite angles because even though I've kind of drawn this one as an extension of F w, it's not necessarily the case. It's a slightly different angle, like that, maybe. Okay. So that's going to be the inverse tangent of the y component of the net force divided by the x component of the net force. So it's the inverse tangent of 212.1 divided by 1412.1 which gives 8.5 degrees. So the net force as a vector -- so I drew this vector symbol over it to mean that we're going to specify magnitude and direction here -- is 1430 newtons, 8.5 degrees from the direction of travel downwind. So this is 8.5 degrees downwind not upwind which would be on the top there. This is downwind, and there we go!