Question
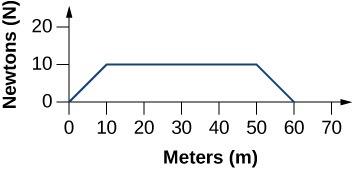
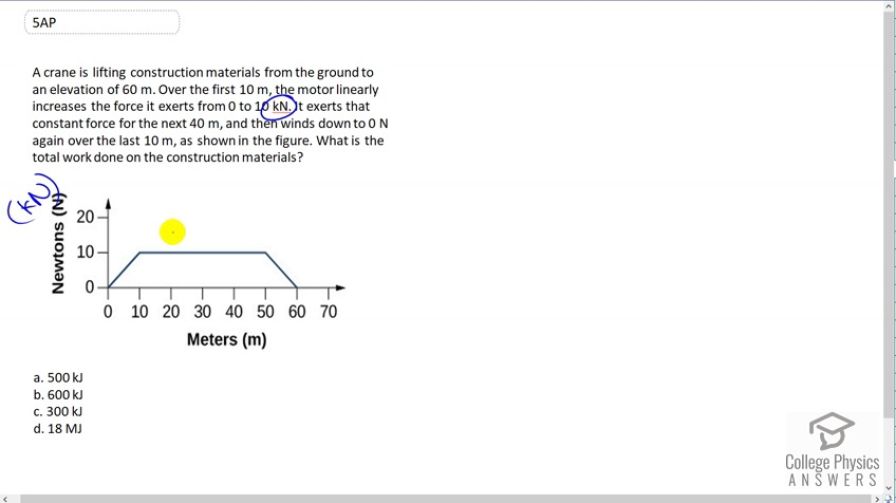
A crane is lifting construction materials from the ground to an elevation of 60 m. Over the first 10 m, the motor linearly increases the force it exerts from 0 to 10 kN. It exerts that constant force for the next 40 m, and then winds down to 0 N again over the last 10 m, as shown in the figure. What is the total work done on the construction materials?
- 500 kJ
- 600 kJ
- 300 kJ
- 18 MJ
Final Answer
(a)
Solution video
OpenStax College Physics for AP® Courses, Chapter 7, Problem 5 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. The total work done by this crane is the area underneath this force displacement curve. So, one thing to notice is that in the question it tells us that the crane has a force that goes from zero to ten kilo-newtons and so in this figure instead of having newtons here, this should say kilo-newtons. So the crane exerts a force that increases linearly from zero to ten kilo-newtons over the first ten meters and we're going to find the area of this triangle. Let's call that area one. It's a triangle with a base of ten meters and a height of ten kilo-newtons, and base times height divided by two is the area of the triangle. So that's 100 divided by two which is 50; kilo-Joules is what that's going to be. Then we have this rectangle, we'll call this area two, with a width of from ten to 50 that makes 40 meters, and a height of ten kilo-newtons. So A two is going to be 40 meters times 10 kilo-newtons which makes 400 kilo-Joules. Then area three is this triangle here, which is the same as area one because it has a height of ten kilo-newtons and a base of ten meters. So A three also equals 50 Joules and the total of all three of these is 50 plus 50 which is 100, that's kilo-Joules there by the way; that's 100 kilo-Joules plus 400 kilo-Joules, makes 500 kilo-Joules. So the answer is A.