Question
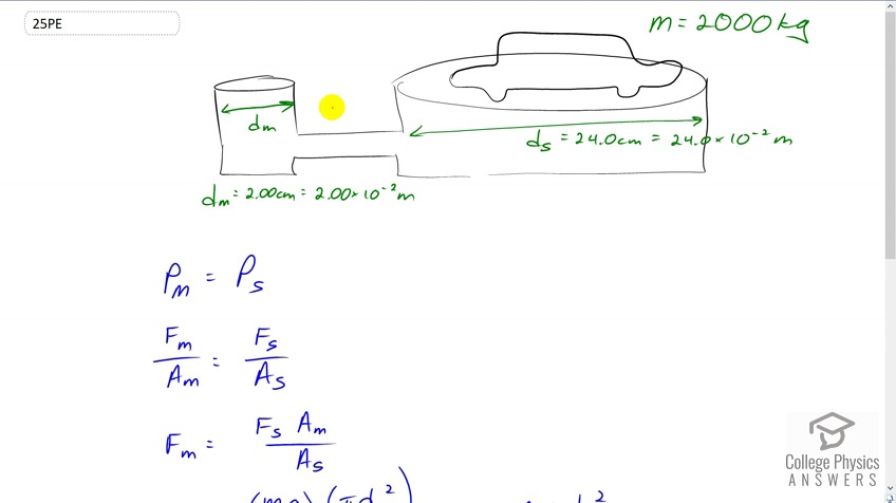
What force must be exerted on the master cylinder of a hydraulic lift to support the weight of a 2000-kg car (a large car) resting on the slave cylinder? The master cylinder has a 2.00-cm diameter and the slave has a 24.0-cm diameter.
Final Answer
Solution video
OpenStax College Physics, Chapter 11, Problem 25 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a master cylinder connected to a slave cylinder by way of this tube, and the pressure in the master cylinder and the slave cylinder has to be the same, that's Pascal's principle. So we're given the diameter of each of these cylinders and knowing that the pressures are the same and knowing the diameter, we can figure out how the forces compare because the force in the master cylinder divided by the area of the master cylinder has to equal the force applied on the surface of this slave cylinder divided by its area. We'll solve for F m by multiplying both sides by the area of the master cylinder. So the force has to be applied downwards on this master cylinder. It's going to be the force the slave cylinder exerts upwards times the area of the master cylinder divided by the area of the slave cylinder. So that's m g is the force that the slave cylinder has to apply, that's the weight of the car times the area of the master cylinder which is pi times its diameter squared over four, divided by pi times diameter of the slave cylinder squared over four. The pi's and the fours there cancel. We're left m g d m squared over d s squared. So that's 2000 kilograms mass of the car, times 9.8 newtons per kilogram, times two centimeters diameter of the master cylinder squared and I've written two centimeters instead of two times ten to the minus two meters, that conversion was not really necessary because I can see that these centimeters squared are going to cancel with the centimeters squared in the denominator and so there is no need to convert them into meters. But if you did convert them into meters, that would be fine. We'll divide all this by 24 centimeters squared which is 136 newtons.


