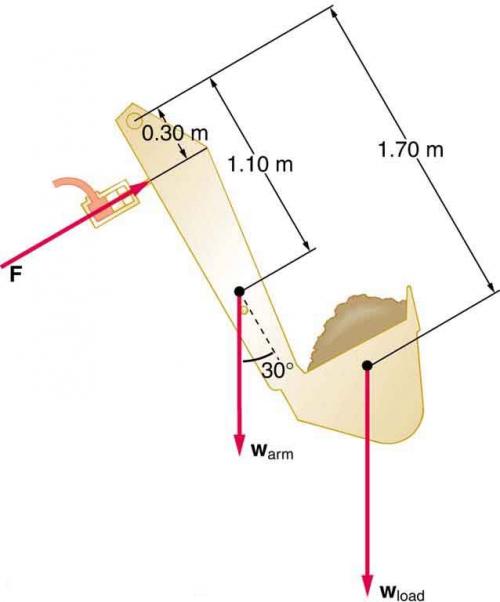
Question
The hydraulic system of a backhoe is used to lift a load as shown in Figure 11.44. (a) Calculate the force the slave cylinder must exert to support the 400-kg load and the 150-kg brace and shovel. (b) What is the pressure in the hydraulic fluid if the slave cylinder is 2.50 cm in diameter? (c) What force would you have to exert on a lever with a mechanical advantage of 5.00 acting on a master cylinder 0.800 cm in diameter to create this pressure?
Final Answer
Solution video
OpenStax College Physics, Chapter 11, Problem 83 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The total counter-clockwise torque and the total clockwise torque has to be equal in order for this back-hoe to support this load. The counter-clockwise torque is exerted by the slave cylinder here, it's exerting a force like this, and it's doing so at this position of 0.3 meters from the pivot which is here. So that's F s for force of the slave cylinder times l s for lever arm of the slave cylinder. These are perpendicular to each other so we didn't need to think about any angles, this is a 90 degree angle there. Then we're going to multiply that by the weight of the arm and find its perpendicular component, perpendicular to the lever arm. So we have this triangle here. This portion here is the perpendicular component, perpendicular to this axis here along the arm of the back-hoe and that's the opposite leg of this triangle. It's the opposite leg, and so we use sine of this angle 30, multiplied by the hypotenuse to find this opposite component. So mass of the arm times g which is the weight of the arm, times sine 30, times the lever arm of the arm, and add to that the clockwise torque due to the load. So here's the weight of the load and then multiply by 30 degrees because these two lines are parallel which means these two angles are corresponding which means this is a 30 degree angle as well. We're going to find the opposite leg of this triangle and that'll be the component of this weight that is perpendicular to the lever arm. There we have that, then we'll divide both sides by l s and factor out the g sine 30 from both terms and you have the force of the slave cylinder is g sine 30 times mass of the arm times lever arm of the arm, plus mass of the load times lever arm of the load, all divided by lever arm of the slave cylinder. So that's 9.81 times sine 30 times 150 kilograms mass of the arm, times 1.1 meters, plus 400 kilograms mass of the load, times 1.7 meters, and all divided by 0.3 meters lever arm of the slave cylinder. This works out to 1.38 times ten to the four newtons. Then the question is, what is the pressure in the hose connected to the slave cylinder? So we know that the force that the slave cylinder has to exert, we've calculated that here in part A, and then we're going to divide that by the area of the cylinder which we're told in part B is two and a half centimeters in diameter, and then the area would be pi times that diameter squared over four. So the pressure is going to be four times the force divided by pi times the diameter of the cylinder squared. So that's four times 1.3816 times ten to the four newtons, divided by pi times two and a half centimeters converted into meters by multiplying by one meter for every 100 centimeters, then you square that result and you get 2.81 times ten to the seven Pascals is the pressure in the hose connected to the slave cylinder. Then suppose we have a lever with a mechanical advantage of five acting on a master cylinder with a diameter of 0.8 centimeters, what force would we have to apply to that lever? So, the pressure in the master cylinder has to be the same as the pressure in the slave cylinder, this is Pascal's law, and so the pressure in the master cylinder is the force exerted by the master cylinder divided by its area. That equals the force, or the -- oops, let's change that to an F, this is the force in the slave cylinder divided by the area of the slave cylinder. Then we can substitute these areas in terms of diameters and we get four F m over pi d m squared equals four F s over pi d s squared -- made a little mistake there. But these fours and these pi's cancel. We're left with F m over d m squared equals F s over d s squared. So the question is, what is the force that we have to apply on a lever connected to this master cylinder? So mechanical advantage is defined as you know, the force that you get on your output divided by the force that has to be applied input. We're told that this equals five. So the force out is five times more than the force in. It's the force in that we're going to be applying. So we can solve this for F out which is the force that the master cylinder has to exert. It's going to be substituted with five times the force input. So we plug that in here and then multiply both sides by d m squared over five, and you get the force input on the lever is the force on the slave cylinder times diameter of the master cylinder squared divided by five, times the diameter of the slave cylinder squared. So we know we're doing things properly probably because we're dividing by the mechanical advantage here. So we expect with a greater mechanical advantage for the force input required to be reduced. So that is the case here as this mechanical advantage goes up in the denominator, that'll be reducing this quotient and thereby reducing the force input. All right. So the force on the slave cylinder is 1.3816 times ten to the four newtons, times the diameter of the master cylinder of 0.8 centimeters and we square that, and divide by five times two and a half centimeters squared. You could convert this into meters if you prefer, that would be the usual routine. Most formulas we convert into meters, kilograms, and seconds, mks units, but in this case I just noticed that we're going to have centimeters squared canceling the centimeters squared and so it wasn't necessary. This works out to 283 newtons.

