Question
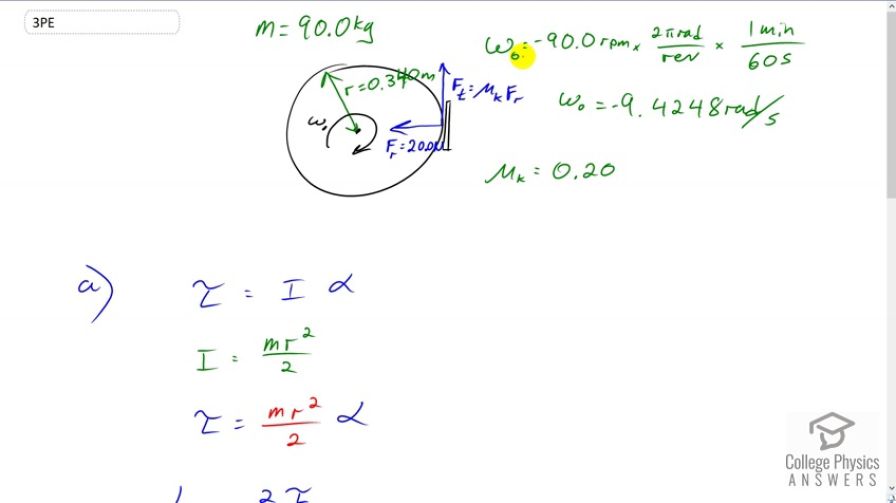
You have a grindstone (a disk) that is 90.0 kg, has a 0.340-m radius, and is turning at 90.0 rpm, and you press a steel axe against it with a radial force of 20.0 N. (a) Assuming the kinetic coefficient of friction between steel and stone is 0.20, calculate the angular acceleration of the grindstone. (b) How many turns will the stone make before coming to rest?
Final Answer
a)
b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 10, Problem 3 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This grinding wheel is spinning in the clockwise direction I suppose which makes it have a negative initial angular velocity. We're told that it's 90 revolutions per minute and we'll convert that into radians per second in order to use this quantity in our calculations. So we multiply by two pi radians per revolution and that cancels the r in rpm. Then we multiply by one minute for every 60 seconds since this is revolutions per minute it's really revs over minutes. So the minutes are in the denominator of this and so the minutes cancel there leaving us with seconds on the bottom. So we have radians per second, negative 9.4248 radians per second. There's an axe head blade which is pressed against the grinding wheel and it's pressed against it in a radial direction which means the grinding wheel will apply a force back on the axe head with a force of equal magnitude and that force will be normal to a tangent here. So that's the normal force that we can use in our friction formula. I wrote F subscript r for radial in our friction formula because the radial force is going to equal this normal force. So the tangential force is going to be the coefficient of kinetic friction multiplied by this radial force with which the blade is pressed against the grinding wheel in a radial direction. Okay. The wheel has a radius of 0.34 meters and a mass of 90 kilograms and part A asks us to figure out what is the angular acceleration of this grinding wheel going to be. So we assume that there is some motor that brought it up to the speed initially and that the motor has now been switched off and the only force causing any angular acceleration is this tangential one due to the friction here. So torque is the moment of inertia multiplied by angular acceleration and we can -- we're going to solve for alpha in a second. But first let's substitute for the moment of inertia. We have to look it up in our book here. It's the same as that for a solid cylinder and that's the total mass of the disk multiplied by its radius squared divided by two. So we substitute that in for i and so torque is m r squared over two times alpha. Now we can solve for alpha by multiplying both sides by two over m r squared. Then we'll switch the sides around as well. So we have alpha equals two times the torque divided by the total mass times radius squared. Now the torque is going to be this tangential force multiplied by the lever arm distance of the pivot which is also known as the radius. So we have the tangential force times the radius is the torque. Now the tangential force though is the force of friction and so it's the radial force multiplied by the coefficient of friction. So we substitute that in and all of this gets replaced in place of tau in our formula for angular acceleration. So angular acceleration is two times the coefficient of friction times the radial force times the radius divided by mass times radius squared. One of the r's cancel and so we have two mu k F r over m r in the end here. So we have two times 0.2 times 20 newtons divided by 90 kilograms times 0.34 meters giving us 0.26 radians per second squared is the angular acceleration. This is a positive acceleration because the acceleration is in the counter-clockwise direction according to the way I've drawn the picture. Now the next question is how many times will the disk rotate during this deceleration? So we're going to figure out the total angular displacement in radians first and then multiply it by one revolution for every two pi radians to get the number of revolutions. So we have the final angular velocity squared equals the initial angular velocity squared plus two times angular acceleration times angular displacement. But the final angular velocity is zero. So we can subtract omega naught squared from both sides and then divide both sides by two alpha. We get this line here. The angular displacement equals the negative of the initial angular velocity squared divided by two times angular acceleration. So it's negative of negative 9.4248 radians per second, squared, divided by two times 0.26144 radians per second squared. We get negative 169.88 radians and then we multiply that by the conversion factor and this gives us negative 27 revolutions. The negative just indicates that the direction of rotation is clockwise based on the way I've drawn the picture.

