Question
A tube is open at one end. If the fundamental frequency f is created by a wavelength λ, then which of the following describes the frequency and wavelength associated with the tube’s fourth overtone?
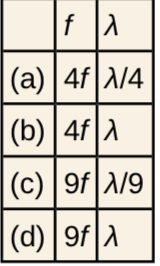
Final Answer
(c)
Solution video
OpenStax College Physics for AP® Courses, Chapter 17, Problem 15 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. For a tube closed at one end, we can see a pattern of the equations for the harmonics. So the first harmonic which is called the Fundamental Frequency will have a one quarter of a wavelength fitting within the length of the tube. Because this is from a node to the first antinode, this is one quarter of the full wavelength which would look like this. And so we can say that the wavelength one is four times L and frequency one being the wave speed divided by lambda is going to be V over four L. So I am deriving some formulas here to show the pattern for frequencies and harmonics in a tube closed at one end. So for the next harmonic that will exist is called the third harmonic just because the integer three is getting multiplied by the fundamental. It is the next frequency that exists. The second harmonic per se does not exist for a tube closed at one end. So in this picture we have three quarters of the third wavelength equal in L. That means the third wavelength then is four L over three. We multiply both sides by four over three here. And that is one third of the fundamental wavelength. So that is four L is the fundamental wavelength. And we dividing it by three. Likewise for the frequency, the third harmonic will be three times V over four L. Because we are going V divided by lambda three which is the same as the multiplying by the reciprocal of lambda three, so multiplying by three over four L in other words. And this is three times the fundamental frequency which was V over four L. And so we have a pattern for the harmonics which is N times the fundamental, where N is one, three, five, seven and so on. Now this is considered the first overtone. And so the first overtone is f subscript three, the third harmonic. And so we can see a pattern for the overtone frequencies. And that the first overtone will be some integer multiplied by f1, where the integer is three, five, seven or nine. And so this is the fourth number in this sequence. And so that's the fourth overtone. And so when we look at this table here, we can see that the fourth overtone is going to be nine times the fundamental. So that narrows it down to either c or d. And so the next question we have to ask you is what is the wavelength of the fourth overtone and the pattern is that the wavelength is going to be the fundamental wavelength divided by whatever this integer is. And so we have the fundamental divided by j. And so for the fourth overtone j is nine and so the answer is lambda over nine. That would be the wavelength associated with the tube's fourth overtone and so the answer is c.