Question
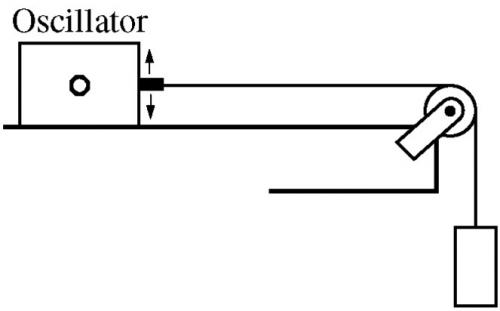
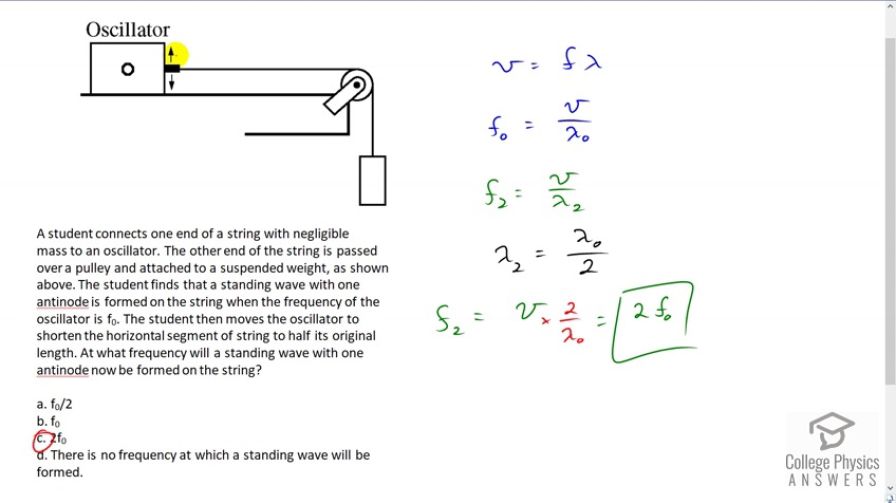
A student connects one end of a string with negligible mass to an oscillator. The other end of the string is passed over a pulley and attached to a suspended weight, as shown above. The student finds that a standing wave with one antinode is formed on the string when the frequency of the oscillator is f0. The student then moves the oscillator to shorten the horizontal segment of string to half its original length. At what frequency will a standing wave with one antinode now be formed on the string?
- There is no frequency at which a standing wave will be formed.
Final Answer
(c)
Solution video
OpenStax College Physics for AP® Courses, Chapter 17, Problem 21 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. So with this set up, we have a mass pulling on a string providing some tension in it, connected to an oscillator and the student measures the fact that there is a wave with one anti-node between the pulley and the oscillator. So an anti-node means there's one peak here in this standing wave and there's a node in each end. And then, the oscillator is moved so that it's closer. And so it moves to a position here. And the question is, what frequency will this new have here. And so that this string length here is half of what it used to be. So we have the wave speed. It's going to be frequency times lambda. And so we can solve for frequency and say that it's wave speed divided by lambda. And so this is the original frequency whatever wave speed divided by lambda naught. And in the second case when the oscillator is moved, the wave speed will stay the same because it is related only to the amount of tension on this string. And so the weight is the same. And so the tension is the same. And so the wave speed is the same. And frequency two will be the same wave speed divided by a new wavelength. And wavelength two is going to be half of the original wavelength, since the oscillator is moved such that the string length is half of what it once was and so we'll substitute this in place of lambda two. And we'll have v divided by lambda two which is the same as multiplying by its reciprocal through multiplying by two over lambda naught. And v over lambda naught is f naught. And so we see that f2 is two times f naught. And so the answer is c.