Question
Mass A has an initial velocity of 22 m/s in the +x-direction. Mass B is three times more massive than mass A and has an initial velocity of 22 m/s in the –x-direction. If the two masses have an elastic collision, what will be the final velocities of the masses after the collision?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 42 (Test Prep for AP® Courses)
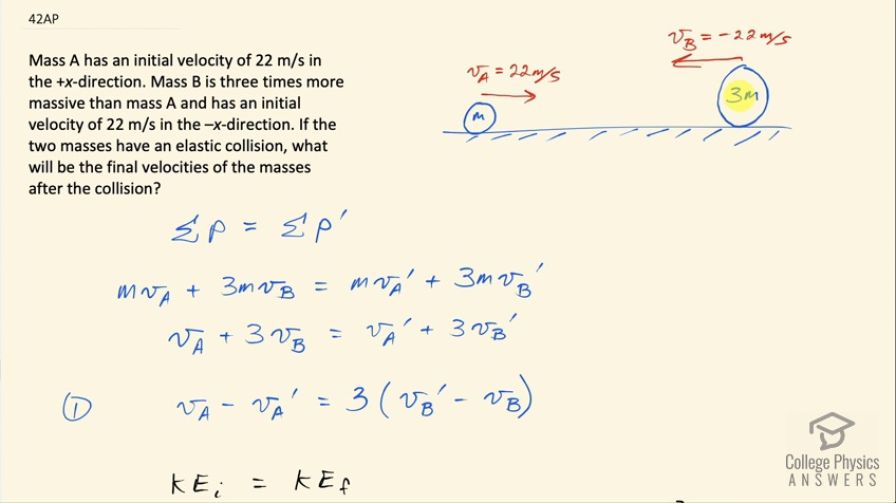
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. Mass A is moving to the right with a velocity of 22 meters per second and mass B, which has a mass 3 times that of A is moving to the left with a velocity of negative 22 meters per second and the question is after an elastic collision, what will the velocities of these two masses be? So we know that the total momentum before collision equals the total momentum after collision and that is mass times velocity A plus 3 times m times velocity B— that's the total momentum before collision— equals mv A prime plus 3mv B prime. Now the masses do not get subscripts A nor B because we are told that this one is 3 times that one so we can just give this a letter and then call this one 3 times that same letter and we don't need to use subscripts A and B anymore and that's convenient because we can divide both sides by m and then we have v A plus 3v B prime equals the velocity of mass A after collision plus 3 times the velocity of mass B after collision. I am going to switch some terms around between the sides of this equation and you will see later why this is strategic— at this point, it's not going to be obvious why I am doing this but I will reveal why later! So we are gonna subtract v A prime from both sides and then also subtract 3v B from both sides. So on the left side, we are left with v A minus v A prime and on the right hand side, we have 3 factored out from the v B prime minus v B that's left over after you factor the factor 3 out from this term and this term. Okay... we'll call that equation number 1 and then we consider the fact that the collision is elastic, which is to say that the total kinetic energy before collision equals the total kinetic energy after collision. So that's one-half mass times v A squared plus one-half times 3m times v B squared equals one-half mv A prime squared plus one-half 3mv B prime squared, the one-half m can be canceled on both sides— let's divide everything by that— and so we have v A squared plus 3v B squared equals v A prime squared plus 3v B prime squared and then we are going to do another trick again to just switch some terms around and we are subtracting v A prime squared from both sides as well as 3v B squared from both sides and we are left with this line here and the reason for all this moving terms around business is to create this difference of squares. We have a subtraction or difference between two terms that are each squared and there's a pattern for factoring that which is to turn it into two binomials where the first binomial has v A minus v A prime and the second binomial has v A plus v A prime and if you were to, you know, multiply through these two binomials, you would end up with this here. And on the right hand side, we have difference of squares as well and it factors into v B prime minus v B times v B prime plus v B all times 3 here and what we are going to do is divide this equation— that we are calling number two— by equation number 1. So equation number 1 was setup this way intentionally so that we would have common factors on the top and bottom when we divided these equations... that was the purpose for moving terms around was strategically knowing that later, we would be factoring this kinetic energy equation into two binomials each to the power of 1 because we want to work with terms that are to the power of 1— working with things that are squared is more challenging. So we are gonna divide through here and on the right hand side, we have 3v B prime minus v B divided by the 3v B prime minus v B that comes from the right hand side of equation 1 and it cancels leaving us with equation that we'll call number 3 v A plus v A prime equals v B prime plus v B. So now we have two equations and there are no squared terms so that's straightforward to solve. We'll rearrange number 3 to solve for v A prime by subtracting v A from both sides. So that's v A prime equals v B prime plus v B minus v A and that can be substituted into equation number 1 so replacing v A prime now with all of this v B prime plus v B minus v A and then distribute the negative sign into here and you get v A minus v B prime minus v B plus v A equals 3v B prime minus 3v B, where I multiplied through by 3 here. And then we are going to add v B prime to both sides (oops) add v B prime to both sides and you have 4v B prime on one side and then we'll add 3v B to both sides which gives us 2v B on the other side and then 2v A's get collected together so after switching the sides around, we have 4v B prime equals 2v A plus 2v B divide both sides by 4 and you get v B prime then is v A plus v B over 2. So that's 22 meters per second is the initial velocity of mass A and then add to that the initial velocity of mass B, which is negative 22 meters per second and that makes 0. So this mass B will stop after the collision. Mass A on the other hand, we have this equation 3 version b to solve for it: we have v B prime is zero now and then add to that v B, which is negative 22 meters per second minus v A so minus positive 22 meters per second, this works out to negative 44 meters per second. So mass A will have the velocity 44 meters per second, to the left after collision.