Question
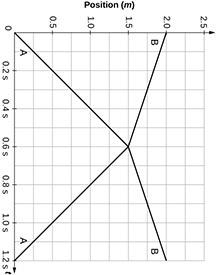
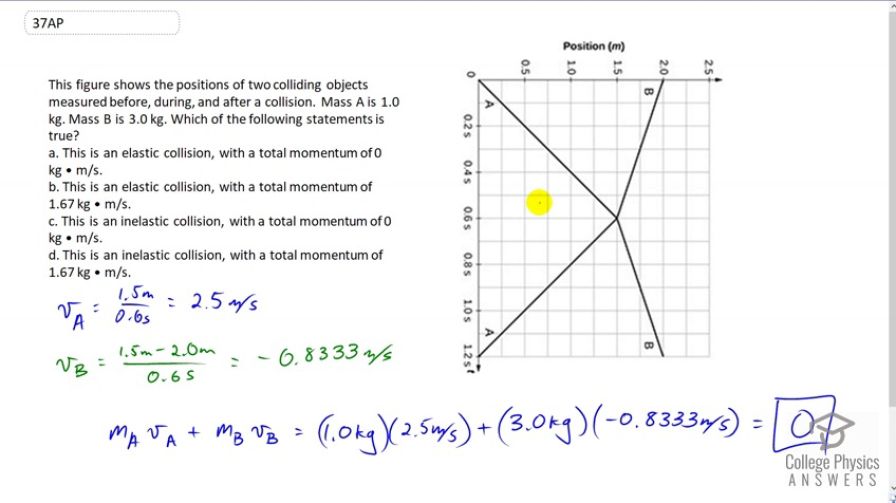
Figure 8.33 below shows the positions of two colliding objects measured before, during, and after a collision. Mass A is 1.0 kg. Mass B is 3.0 kg. Which of the following statements is true?
- This is an elastic collision, with a total momentum of 0 kg • m/s.
- This is an elastic collision, with a total momentum of 1.67 kg • m/s.
- This is an inelastic collision, with a total momentum of 0 kg • m/s.
- This is an inelastic collision, with a total momentum of 1.67 kg • m/s.
Final Answer
(a)
Solution video
OpenStax College Physics for AP® Courses, Chapter 8, Problem 37 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We're given a graph of position versus time for two objects that are colliding. Mass A has a mass of one kilogram and mass B is three kilograms. One thing that is important to notice about this picture is that it's not showing the path taken by the two objects. They're not moving like this and then colliding here. They're colliding at this time but not at this position here on the graph. Well, I mean -- let me illustrate what I mean. So this is actually a one dimensional collision, a head-on collision between two things moving along a line. So mass A starts at a position that we define as zero and so this is x equals zero. Mass B begins at a position of two. Mass B is bigger, it's three kilograms. So this position is x equals two and they're moving towards each other. They move toward each other for 0.6 seconds at which time they collide. So they collide here but it's not really important to know -- well, I guess it is kind of important to know where they collide. They collide at a position of 1.5 meters. So if this is zero and this is two, they collide approximately here,. x equals 1.5. So block B is moving more slowly and only reaches -- it only covers this distance in the time it takes mass A to cover this whole distance here. Okay. So, we can say a couple of things here. We can say that -- we can find the total momentum in this scenario by figuring out what the velocities are of each of these blocks. We can tell that block A has a final position of 1.5 meters, then minus its initial position of zero means it has a change in position of 1.5, divided by the 0.6 seconds it takes to get there to the collision. So its velocity is 2.5 meters per second. Object B has a final position of 1.5 after its collision minus 2.0 meters, its initial position. So that's negative 0.5 change in position divided by 0.6 which gives a velocity of negative 0.8333 meters per second. Now, we can also tell that the velocities of each of these blocks are the same after the collision. You know, it covers 1.5 meters in 0.6 seconds again after the collision for mass A and mass B likewise covers the same 0.5 meters in 0.6 seconds after the collision, just as it did before the collision. So since the masses of course remain the same and the velocities -- well the speeds are the same that means kinetic energy is conserved. So this is an elastic collision so that narrows it down to options A and B. Now to figure out the total momentum we'll have to use these velocities that we calculated to figure out what the total momentum is of the system. So we have mass A times velocity A plus mass B times velocity B. So that's one kilogram times 2.5 meters per second plus three kilograms times negative 0.8333 meters per second. This adds up to zero and so the answer is A.