Question
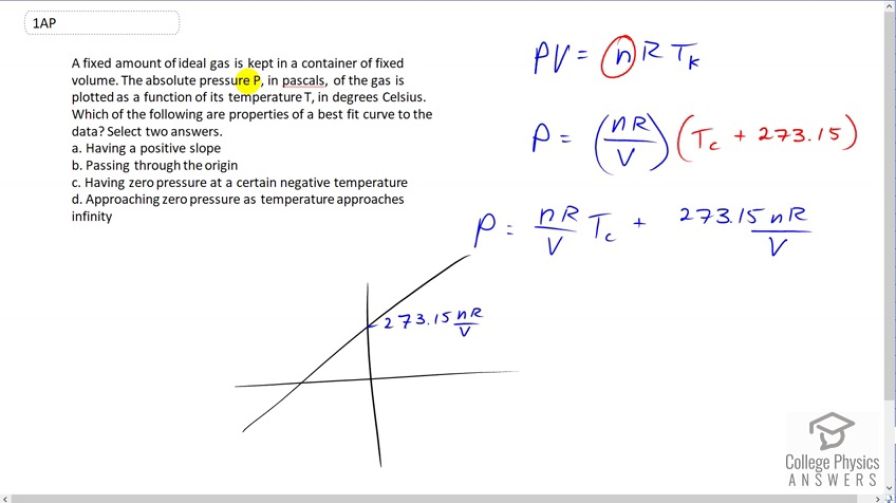
A fixed amount of ideal gas is kept in a container of fixed volume. The absolute pressure P, in pascals, of the gas is plotted as a function of its temperature T, in degrees Celsius. Which of the following are properties of a best fit curve to the data? Select two answers.
- Having a positive slope
- Passing through the origin
- Having zero pressure at a certain negative temperature
- Approaching zero pressure as temperature approaches infinity
Final Answer
(a) and (d)
Solution video
OpenStax College Physics for AP® Courses, Chapter 13, Problem 1 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. A fixed amount of ideal gas which in a fixed amount means that the number of moles did not change, it's kept in a container of fixed volume. So V does not change either. And the absolute pressure of the gas is plotted as a function of temperature in degree Celsius and that's an important point here actually. So we're going to rewrite this ideal gas law and as a function of temperature or solve for pressure as a function of temperature by dividing both sides by V. And then we're also going to substitute for this absolute temperature with the Celsius temperature. So we'll write Celsius temperature plus 273.15 in place of absolute temperature. And then if you multiply through by this nR over V, we get the pressure is nR over V times the temperature in Celsius plus 273.15 times nR over V. And this is a linear function with a y-intercept equal to this. And the slope of this line is going to be nR over V. And so we can figure out which answers to choose now that we have this formula. And so it's going to have a positive slope because the number of moles is positive and so is the gas constant and so is the volume. And it does not pass through the origin, in fact at x equals zero, this is going to be the value of the pressure. And then, it will have a zero pressure though at a certain negative Celsius temperature as you can see from this line. And so c is also an answer.