Question
What is the average kinetic energy of a nitrogen molecule () if its rms speed is 560 m/s? At what temperature is this rms speed achieved?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 13, Problem 7 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
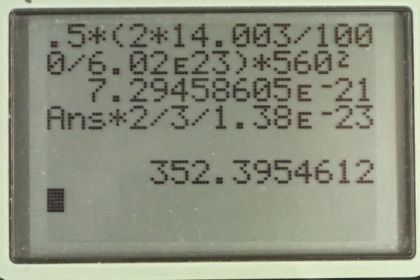
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the average kinetic energy of a Nitrogen molecule at an rms speed of 560 meters per second and figure what temperature this rms speed happens. So average kinetic energy is one half times mass times the average velocity squared. So it's one half times the mass of a single Nitrogen molecule, and Nitrogen molecule is N2. And so there's two Nitrogen atoms and the molar mass of each Nitrogen is 14.003 grams per mole. Let me convert that into kilograms per atom by multiplying by one kilogram per 1000 grams and then multiplied by one mole for every 6.02 times ten to the 23 molecules. So I should have said that this is molecule, this is a mass of a single molecule of Nitrogen consisting of two Nitrogen atoms. Then we times by 560 meters per second and we square that and this gives a kinetic energy of 7.29 times ten to the minus 21 Joules for each Nitrogen molecule. Now the temperature at which this kinetic energy would occur is what we can figure out from this formula saying that the average kinetic energy is three over two times the Boltzmann Constant times temperature. And we'll solve for T by multiplying both sides two over three k. So temperature is two times the average kinetic energy divided by three times Boltzmann Constant. So that's two times the answer we got before for the number of Joules for each of the molecule divided by three times Boltzmann Constant, giving us a temperature of 352 Kelvin.