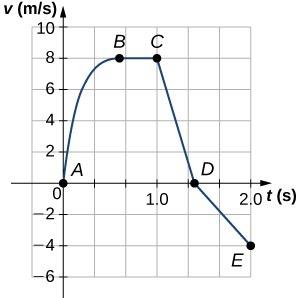
Figure 2.81 Graph showing Velocity vs. Time of a cart. A cart is constrained to move along a straight line. A varying net force along the direction of motion is exerted on the cart. The cart's velocity v as a function of time t is shown in the graph. The five labeled points divide the graph into four sections. Which of the following correctly ranks the magnitude of the average acceleration of the cart during the four sections of the graph? (a) $a_{CD}>a_{AB}>a_{BC}>a_{DE}$
(b) $a_{BC}>a_{AB}>a_{CD}>a_{DE}$
(c) $a_{AB}>a_{BC}>a_{DE}>a_{CD}$
(d) $a_{CD}>a_{AB}>a_{DE}>a_{BC}$

Video Transcript

This is College Physics Answers with Shaun Dychko. When I looked at this question, I looked at the section where the velocity-time graph is horizontal and I said well that is going to be the lowest acceleration because with velocity not changing at all, between this time and this time, that means this is going to be the lowest ranking acceleration; acceleration would be zero between (b) and (c). And then when you look at these different options here, there's only one that has acceleration BC listed as the smallest so (d) is gonna be the answer. So if you get lucky, you need to look at only that and you are done but we could double check to confirm that this is correct. We can find the greatest acceleration and we do that by looking for the largest change in velocity which is from 0 up to 8 and that change in velocity occurs between A and B and it also occurs between points C and D. Now that's the change in velocity and the interval which has the smallest amount of time will be the higher acceleration. So this change in velocity occurs over 1.3 seconds here, more or less, or sorry 0.3 seconds so from 1 to 1.3 so that's a change in time of 0.3 seconds here between C and D and whereas between A and B, it takes about almost 0.6 seconds— each tick mark here is 0.3 seconds here. So this same change in velocity from 0 to 8 or from 8 to 0 occurs between points A and B and C and D but between C and D, it occurs more quickly and so that acceleration is going to be higher. So a acceleration between C and D is going to be the greatest acceleration and so (d) also checks out with that fact. And then these other acceleration's should be somewhere in between but we already have enough information here to tell us that (d) is the answer.