Question
When non-metric units were used in the United Kingdom, a unit of mass called the pound-mass (lbm) was employed, where 1 lbm = 0.4539 kg . (a) If there is an uncertainty of 0.0001 kg in the pound-mass unit, what is its percent uncertainty? (b) Based on that percent uncertainty, what mass in pound-mass has an uncertainty of 1 kg when converted to kilograms?
Final Answer
- or
Solution video
OpenStax College Physics for AP® Courses, Chapter 1, Problem 26 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
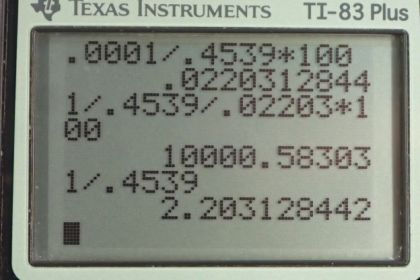
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A pound mass is 0.4539 kilograms and we are told that the error in this unit is about 0.0001 kilograms and part (a) asks us what percent uncertainty does this absolute uncertainty represent? So we take the absolute uncertainty divided by measurement times a 100 percent. So for every 0.4539 kilograms, which is 1 pound mass, there is 0.0001 kilograms of air so we divide those two times by a 100 percent and we get 0.02203 percent which we round to one significant figure because this has one significant figure and error's always have one or maybe two significant figures. So 0.02 percent is the percent uncertainty in this pound mass unit. Part (b) says how many pound masses would you have if the error was 1 kilogram? And so we replace this... well, first we have to rearrange this uncertainty formula which is equation 8 in chapter 1. We rearrange this to solve for A so we multiply both sides by A and divide both sides by the percent uncertainty and so we have things canceling here and we are left with A equals the absolute error in A divided by percent uncertainty times 100 percent. So the error is 1 kilogram and we'll convert that into pound mass so that we get an answer A in units of pound mass. So 1 kilogram times 1 pound mass for every 0.4539 kilograms divided by the percent uncertainty we found in part (a), 0.02203, and I'm using the unrounded number to avoid intermediate rounding error we are not gonna put 0.02 percent there, we'll use 0.02203 percent times a 100 percent and we get 10000.583 pound mass. Now the question is what should this be rounded to and the answer will come from what is the place value of the error? So the error is 1 kilogram and we convert that into pound mass here and we end up with 2 pound mass so this has precision to the one's place and so that means this should have precision to the one's place as well which means this should be rounded to a 1 there, okay. So this is 1.0001 times 10 to the 4 pound mass or without scientific notation, you could have also said 10001 pound mass, that would also be fine. There we go!