Question
A marathon runner completes a 42.188 km course in 2 h, 30 min, and 12 s. There is an uncertainty of 25 m in
the distance traveled and an uncertainty of 1 s in the elapsed time. (a) Calculate the percent uncertainty in the distance. (b) Calculate the uncertainty in the elapsed time. (c) What is the average speed in meters per second? (d) What is the uncertainty in the average speed?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 1, Problem 24 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
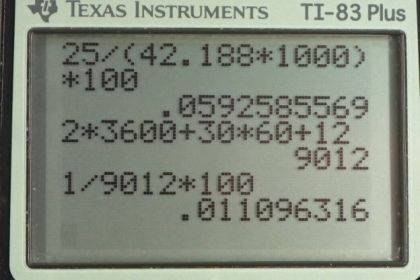
This is College Physics Answers with Shaun Dychko. A marathon runner runs 42.188 kilometers and the uncertainty in this distance is 25 meters and it takes them 2 hours, 30 minutes and 12 seconds and the uncertainty in that time is 1 second. So part (a) asks us to find the percent uncertainty in the distance. So we have to take the uncertainty in the distance that is the absolute uncertainty, number of meters, divided by the total distance, also in meters; we need to have units in top and bottom the same and that's an important point here because the distance is given to us in kilometers and the absolute error in the distance is given in meters. So we have 25 meters error divided by 42.188 kilometers times 1000 meters for every kilometer giving us units of meters on the bottom times a 100 percent giving us 0.059 percent is the error. In an error, you sometimes have one significant figure or maybe two but never three because this is just an estimate of what your error is and you can't be very precise in something that is itself just a guess anyway and I chose to—just because our error is given in two significant figures here, 25 meters has two significant figures— so I chose for it to have two significant figures in the percent uncertainty. And part (b) asks us what is the percent uncertainty in the time? So we take the uncertainty in the time divided by the time times 100 percent. So the units have to be the same and this time is given in a strange format here, 2 hours 30 minutes and 12 seconds. We want to express all of this in seconds so that it has the same units as the error which is in seconds. So we have 2 hours times 3600 seconds per hour so the hours cancel so that's 7200 seconds plus 30 minutes times 60 seconds per minute and that gives us some number of seconds there plus 12 seconds for a total of 9012 seconds. So the percent uncertainty then is 1 second error divided by total number of seconds of 9012 times 100 percent giving us 0.01 percent error and I have one significant figure here because this error has one significant figure there. Then we are going to find the speed of the marathon runner in meters per second so we take the distance traveled, 42.188 kilometers, convert it into meters by multiplying by 1000 meters for every kilometer and divide by the total time of 9012 seconds giving 4.6813 meters per second. Now it's not strictly clear how many significant figures we should have in our answer and one way to take a guess is to look at these numbers here and since this is division, the result of dividing is the same rule as for multiplying where you have as many significant figures in the answer as the least precise number that you are working with and so this one has only four significant figures whereas this one has five and so we take the fewest number of significant figures among these answers or among these numbers and that's the number of significant figures in our answer so this one has four, this one has five and so our answer should have four probably. Now a more rigorous or a better way, you could say, for determining the number of significant figures has to do with figuring out what is the percent error in this number. Well, first we find the percent error and then we find the absolute error and we'll round this number so that it has the same precision as the error does. So if you use this rule of, you know, number of significant figures that would be fine and usually, that's what you are going to do but since we are given errors in these numbers, an even better way is part (d) so let's do that now. When dividing two numbers, the percent error and the answer— speed in this case— is going to be the sum of the percent errors of the numbers you are working with so the percent error in the distance plus the percent error in the time. So that's 0.05925 percent error in distance and I'm using lots of digits here to avoid intermediate rounding error— you always use unrounded numbers in subsequent calculations— so I'm not gonna use 0.059 like I had for the answer in part (a), I'm using 0.05925, and then add to that the percent error in time, 0.011096, to get a total of 0.07035 percent. And now that's just part of this answer here; we want to find the absolute error in the speed plus or minus how many meters per second. So the error in the speed then is gonna be the speed itself multiplied by its percent error divided by 100 percent and so that's 4.6813 meters per second times 0.07035 percent error divided by 100 percent giving 0.00329 meters per second. Now this should be rounded to one significant figure as most errors will be and so the error is 0.003 meters per second. Now this informs what place value we should round our answer for speed to and since this error is in this place value— that's the thousandths— that means our answer up here should also be rounded to the thousandths and it turns out that using this analysis of figuring out the error in our quotient or the result of our division, finding this error gives us the same number of significant figures as this sort of back of the hand or back of the envelope I should say method of counting the number of significant figures in each factor and we said it should have four because 9012 seconds has four significant figures and so we wrote four significant figures here and that turned out to be just the same as this more rigorous analysis here which said also round to the thousandths place which ends up giving us four significant figures as well.