Question
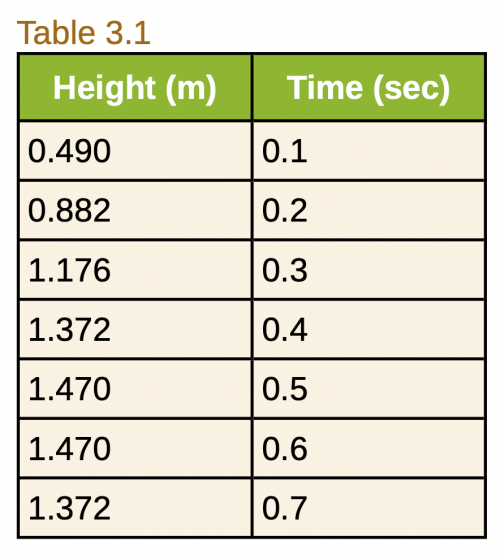
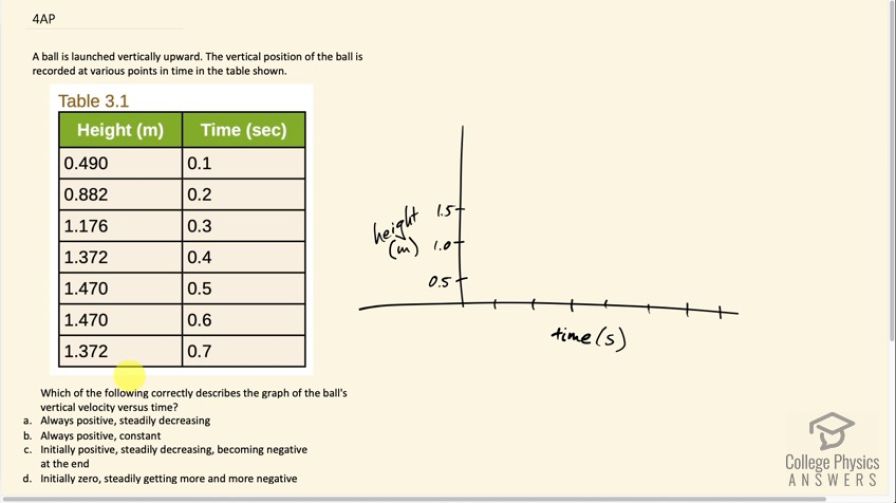
A ball is launched vertically upward. The vertical position of the ball is recorded at various points in time in the table shown.
Which of the following correctly describes the graph of the ball's vertical velocity versus time?
- Always positive, steadily decreasing
- Always positive, constant
- Initially positive, steadily decreasing, becoming negative at the end
- Initially zero, steadily getting more and more negative
Final Answer
(c)
Solution video
OpenStax College Physics for AP® Courses, Chapter 3, Problem 4 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. A ball is launched vertically straight upwards and the vertical position is recorded at various points in time. We only need to do a rough graph here because we want to just have a graph that's good enough to pick one of these four options as to what describes the ball's vertical velocity versus time. The velocity is going to be the slope of this position time graph. If we make a rough sketch of the graph, we'll be able to examine its slope here. At 0.1 second, it's about 0.5 meters, so we can put a point there. At 0.2 seconds, it's about 0.8. At 0.3, a little bit above 1. At 0.4, it's 1.4. At 0.5, it's almost 1.5. Then at 0.6, it's the same. This is 1.47. Then at 0.7, it started to go back down and its vertical position is 1.37. If we consider the slope at various times here, we can see that initially the slope is positive and fairly steep. But once we get to times like 0.5, at 0.6, the slope is horizontal, in which case the velocity then is zero, which we expect because when the ball is going upwards, it eventually, if it starts here, say, and the ball is going upwards, as it gets to this maximum height here, it'll have a moment of having zero velocity as it changes direction to go back down. That's this time here somewhere in between point 0.5 and 0.6 seconds, it reached a zero velocity, instantaneous velocity. Then it goes downwards from that point on, and so it has a negative velocity here. This is a negative slope. Let's find out which of these options fits that description. It's not always positive because we just said it's negative at this time. Neither A nor B. Initially positive steadily decreasing, becoming negative at the end. C is the answer to this question.