Question
(a) What is the uncertainty in the energy released in the decay of a due to its short lifetime?
(b) What fraction of the decay energy is this, noting that the decay mode is (so that all the mass is destroyed)?
Final Answer
Solution video
OpenStax College Physics, Chapter 33, Problem 19 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
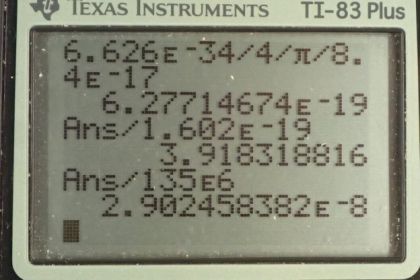
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Heisenberg uncertainty principle says that the product of the uncertainty in energy and time is greater than or equal to the Planck's constant divided by 4π and so we'll find the minimum possible uncertainty in energy by dividing both sides by Δt and we get that the uncertainty in energy is at least h over 4π Δt. And so that is Planck's constant divided by 4π times the lifetime of this particle which is 8.4 times 10 to the minus 17 seconds which we found in table [33.2]. And converting that into electron volts by multiplying by 1 electron volt for every 1.602 times 10 to the minus 19 joules, we get 3.9 electron volts is the minimum uncertainty in the energy. And we are told that this pion decays into two photons and the total energy then is gonna be 135 megaelectron volts and so what fraction does this uncertainty represent of this total mass energy of the particle? So we have 3.9 electron volts divided by 135 times 10 to the 6 electron volts which is a fraction of 2.9 times 10 to the minus 8.