Question
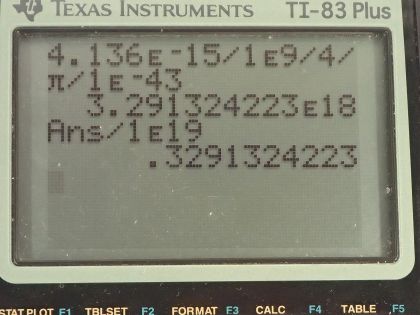
(a) Use the Heisenberg uncertainty principle to calculate the uncertainty in energy for a corresponding time interval of . (b) Compare this energy with the unification-of-forces energy and discuss why they are similar.
Final Answer
Solution video
OpenStax College Physics, Chapter 34, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have to use the Heisenberg uncertainty principle to calculate the uncertainty in energy given an uncertainty in time of 10 to the minus 43 seconds. So the Heisenberg uncertainty principle says take the product of uncertainty in energy and the uncertainty in time and that is well greater than or equal to Planck's constant over 4π. And we can divide both sides by the uncertainty in time and get the uncertainty in energy then at its minimum is equal to Planck's constant over 4π times the uncertainty in time. So Planck's constant is 4.136 times 10 to the minus 15 electron volt seconds and I am going to convert this into gigaelectron volt seconds because in part (b), we are meant to compare this energy with 10 to the 19 gigaelectron volts. So we divide that by 4π times 10 to the minus 43 seconds and we get 3 times 10 to the 18 gigaelectron volts. When we compare that with 10 to the 19 gigaelectron volts, this is 0.3 or smaller by a factor of 0.3. And this is the unification-of-forces energy and this time is close to the Planck time— the minimum possible interval of time and we expect all the forces to be unified at the Planck time and this is getting close to it and so we see that it is getting close to the unification energy.