Question
(a) At what speed would a airplane have to fly to have a momentum of (the same as the ship’s momentum in the problem above)? (b) What is the plane’s momentum when it is taking off at a speed of ? (c) If the ship is an aircraft carrier that launches these airplanes with a catapult, discuss the implications of your answer to (b) as it relates to recoil effects of the catapult on the ship.
Final Answer
a)
b)
c) The ship will recoil with the same momentum, but it's recoil speed will be much less since it is much more massive.
Solution video
OpenStax College Physics, Chapter 8, Problem 3 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
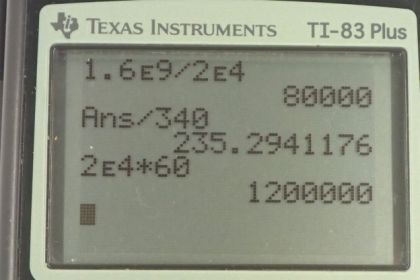
This is College Physics Answers with Shaun Dychko. In order to have a momentum of 1.6 times ten to the nine kilogram meters per second, the airplane with mass two times ten to the four kilograms, would need to have a speed of 8.00 times ten to the four meters per second in order to have that momentum. We figured this out by saying momentum is mass times velocity then dividing both sides m to solve for v. Now this is an unrealistic number because this is Mach 235 if you take this number and divide it by the speed of sound which is 340 meters per second. That's how you get the Mach number and there are no planes that can go that speed. In part B, well what would the momentum be if the plane's launch velocity was 60 meters per second? So we have the same mass multiplied by 60 and that gives 1.2 times ten to the six kilogram meters per second. In part C, it asks suppose there is an aircraft carrier that is launching this plane using a catapult and what will happen to the ship? The answer is it will recoil with the same momentum backwards as the plane is going forwards but its recoil speed will be much, much less than the speed of the plane because the ship is very, very much more massive than the plane.